Det grundlæggende netværk teoremer brugt i netværksanalyse er tilgængelige i forskellige typer som Thévenin's, superposition, Norton's, substitution, maksimal magtoverførsel, gensidighed og Millmans teoremer . Hvert teorem har sine egne anvendelsesområder. Så det er meget vigtigt at forstå hver netværkssætning, fordi disse teoremer kan bruges gentagne gange i forskellige kredsløb. Disse teoremer hjælper os med at løse komplekse netværkskredsløb for en given tilstand. Denne artikel diskuterer en af typerne af netværkssætning substitutionssætning – eksempler.
Hvad er substitutionssætningen?
Udsagn om substitutionssætning er; at når strømmen gennem grenen eller spændingen over en hvilken som helst gren i et netværk er kendt, så kan grenen ændres ved kombinationen af forskellige elementer, der vil lave den samme spænding og strøm i hele grenen. Det kan med andre ord defineres som; den termiske spænding, såvel som strøm, bør være identisk for ækvivalens af gren.
Substitutionssætningsbegrebet afhænger hovedsageligt af substitution af et element med et andet element. Denne sætning er også meget nyttig til at bevise nogle andre sætninger. Selvom denne sætning ikke er anvendelig til at løse sætningen, som omfatter de to ovennævnte kilder, som hverken er serieforbundet eller parallelt.
Forklaring af substitutionssætning
De trin, der er involveret i løsningen af substitutionssætningen, omfatter hovedsageligt følgende.
Trin 1: Først skal vi finde spændingen og strømmen af alle netværkselementerne. Generelt kan spændingen og strømmen beregnes ved hjælp af ohms lov, Kirchoffs love som KVL eller KCL.
Trin 2: Vælg den nødvendige gren, som du ønsker at fjerne gennem et andet element som spændingskilde/modstand og strømkilde.
Trin 3: Find den rigtige værdi af det erstattede element, forudsat at spændingen og strømmen ikke ændres.
Trin 4: Tjek det nye kredsløb ved blot at beregne strømmen og spændingen for alle elementer og evaluere det af det originale netværk.
Substitutionssætnings kredsløbsdiagram
Lad os let forstå substitutionssætningen ved at bruge følgende kredsløbsdiagram. Vi ved, at substitutionssætningen er erstatningen af et enkelt element med et andet ækvivalent element. Hvis et element i et netværk udskiftes/erstattes med en strømkilde eller spændingskilde, hvis strøm og spænding gennem eller på tværs af elementet vil forblive uændret som det tidligere netværk.
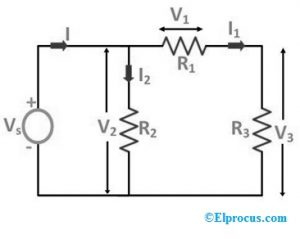
De forskellige modstande som R1, R2 & R3 er forbundet simpelthen over spændingskilden. Strømmen af strøm 'I', der flyder gennem kredsløbet, er adskilt i I1 & I2, hvor 'I1' leveres gennem 'R1'-modstanden, og 'I2' strømmer gennem R2-modstanden som vist i kredsløbet. Her falder spændingsfaldet over modstandene R1, R2 & R3 er V1, V2 & V3 tilsvarende.
Hvis 'R3'-modstanden nu erstattes af 'V3'-spændingskilden som vist i følgende kredsløbsdiagram nedenfor:
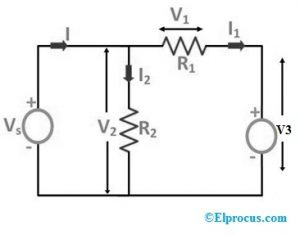
I det følgende kredsløbsdiagram erstattes 'R3'-modstanden af strømmen gennem hele elementet 'I1'.
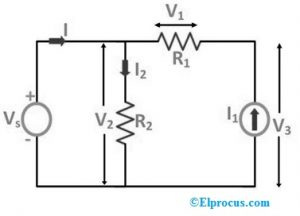
Fra ovenstående to tilfælde, hvis elementet erstattes med strøm- eller spændingskilden, ændres kredsløbets startbetingelser ikke, hvilket betyder, at spændingsforsyningen over modstanden og strømforsyningen gennem modstanden ikke ændres, selvom de erstattes med andre kilder.
Eksempler på problemer
Eksempler på substitutionssætningsproblemer diskuteres nedenfor.
Eksempel 1:
Løs følgende kredsløb med substitutionssætningen for at beregne spændingen og strømmen inden for alle modstandene.
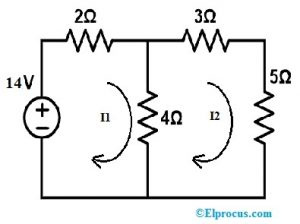
Trin 1:
Anvend først KVL til loop1 i ovenstående kredsløb
14 = 6I1 – 4I2 ….(1)
Anvend KVL til loop2 i ovenstående kredsløb
0 = 12I2 – 4I1
12 I2 = 4I1 => I1 = 3I2……….(2)
Erstat denne ligning 2 i ovenstående ligning 1.
14 = 6(3I2) - 4I2
14 = 18I2 – 4I2 =>14I2 => 1A
I2 = 1A
Fra ovenstående ligning-(2)
I1 = 3I2
Vi ved, at I2 = 1A
I1 = 3A
Trin 2:
I dette trin skal vi fjerne loop1-grenene for at lave en enkelt løkke.
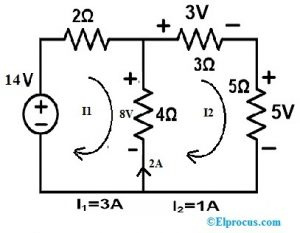
Trin 3:
Vi kan placere en strømkilde/spændingskilde i stedet for 4Ω modstanden. Nu vil vi bruge en aktuel kilde.
Strømmen gennem loop2 i kredsløbet er 1A. Så vi erstatter grenen med 1A strømkilde. Som et resultat er det resterende kredsløb vist nedenfor.
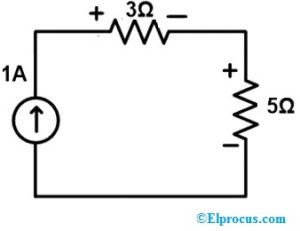
Trin 4:
I dette trin skal du kontrollere spændingen og strømmen af alle elementerne. Ovenstående kredsløb inkluderer en enkelt sløjfe, dvs. en strømkilde. Værdien af strømmende strøm gennem løkken svarer således til den aktuelle kildeværdi.
Her er den aktuelle kildeværdi 1A. Så strømmen af strøm gennem 3Ω & 5Ω modstandsgrenene er 1A, hvilket svarer til det originale netværk.
Ved at bruge ohm lov , find spændingsværdien over 3Ω modstanden
V = IS
V = I x R
V = 1 x 3 => 3V.
På samme måde skal vi ved at bruge ohm-loven finde spændingsværdien over 5Ω modstand.
V = IS
V = I x 5
V = 1 x 5 => 5V.
Strømmen og spændingen svarer således til det originale netværk. Så det er sådan denne teorem virker.
Hvis vi nu vælger spændingskilden i stedet for strømkilden i trin 3. Så i denne tilstand svarer spændingskildens værdi til 4Ω modstandsgrenværdien.
Strømmen i hele 4Ω modstandsgrenen inden for det originale netværk er
I1 – I2 => 3 – 1 => 2A
Ifølge Ohms lov;
Spændingen ved 4Ω modstand er V = 2 x 4 = 8V
Så vi skal forbinde spændingskilden med 8V i netværket, og det resterende kredsløb er vist i nedenstående diagram.
V= 2 x 4 = 8V
Så vi skal forbinde 8V spændingskilden med netværket, og det resterende kredsløb er som vist i nedenstående figur.
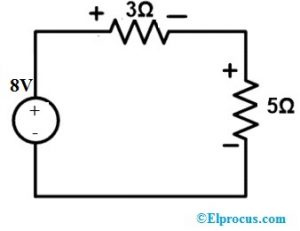
Anvend KVL til ovenstående sløjfe for at verificere spændingen og strømmen.
8 = 3I + 5I => 8I
I = 1A.
Ved at bruge ohm-loven kan spændingen over modstanden 3Ω beregnes som;
V = 1 × 3 => 3V
På samme måde er spændingen over modstanden 5Ω;
V= 1 × 5 => 5V
Spændingen og strømmen er således den samme efter substitution som det oprindelige netværk.
Eksempel 2:
Lad os tage følgende kredsløb for at anvende substitutionssætningen.
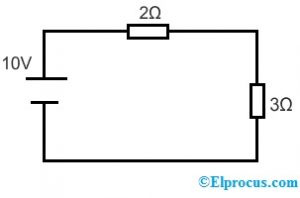
Ifølge spændingsdelingslinealen er spændingen over 2Ω & 3Ω modstande;
Spændingen ved 3Ω modstanden er
V = 10×3/3+2 = 6V
Spændingen ved 2Ω modstanden er
V = 10×2/3+2 = 4V
Strømmen i hele kredsløbet beregnes som I = 10/3+2 = 2A.
I ovenstående kredsløb, hvis vi erstatter en 6V-spændingskilde i stedet for 3Ω-modstanden, vil kredsløbet blive som følgende.
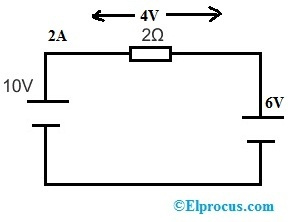
Baseret på Ohms lov er spændingen over 2Ω-modstanden og strømstrømmen gennem kredsløbet
V = 10-6 => 4V
I = 10-6/2 = 2A
Hvis vi erstatter en 2A strømkilde i stedet for en 3Ω modstand, vil kredsløbet blive som følgende.
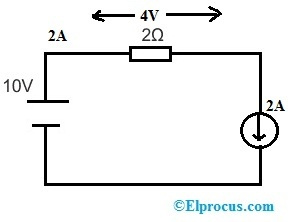
Spænding over 2Ω modstand er V = 10 – 3* 2 => 4 V & spænding over ’2A’ strømkilde er V = 10 – 4 => 6 V. Så spændingen over 2Ω modstand & strøm i hele kredsløbet ændres ikke.
Fordele
Det fordelene ved substitutionssætningen omfatte følgende.
- Dette sætningsbegreb afhænger hovedsageligt af substitutionen af et enkelt element fra et andet element.
- Denne teorem giver intuition om kredsløbsadfærden og hjælper også med at verificere forskellige andre netværkssætninger.
- Fordelen ved at bruge denne sætning er, at denne sætning giver de korrekte værdier for de variable som X & Y, der svarer til skæringspunktet.
Begrænsninger
Det substitutionssætningens begrænsninger omfatte følgende.
- Denne teorem kan ikke bruges til at løse et netværk, der omfatter minimum to eller flere kilder, der ikke er inden for serie/parallel.
- I denne sætning bør kredsløbsadfærden ikke ændre sig, når elementet udskiftes.
Ansøgninger
Det anvendelser af substitutionssætningen omfatte følgende.
- Substitutionssætningen bruges til at bevise adskillige andre sætninger.
- Denne teorem er nyttig til at løse ligningssystemet i matematik.
- Denne sætning erstatter kredsløbets ene element med et element mere.
- Denne teorem bruges til at analysere kredsløbene med afhængige kilder.
På hvilket kredsløbs substitutionssætning er ikke anvendelig?
Kredsløbet som har de to ovenstående kilder, der er forbundet enten parallelt eller i serie, så er denne substitutionssætning ikke anvendelig.
Hvorfor kaldes kompensationsteorem substitution?
Begge teoremer som kompensation og substitution er identiske med hensyn til procedure og reduktion. Så denne sætning er anvendelig for antenner og kaldes også substitutionssætningen.
Hvordan bruger du substitutionssætningen?
Denne sætning kan bruges ved at erstatte enhver gren med en anden gren inden for et netværk uden at forstyrre spændingerne og strømmene i hele netværket. Så denne teorem bruges i både lineære og ikke-lineære kredsløb.
Hvad er substitutionsegenskab?
Substitutionsegenskaben angiver, at hvis en variabel 'a' er ækvivalent med en anden variabel 'b', så kan 'a' erstattes i stedet for 'b' i ethvert udtryk eller ligning, og 'b' kan erstattes i stedet for ' a' i ethvert udtryk eller ligning.
Det handler altså om en oversigt over en substitution sætning – kredsløb med eksempler. Her er et spørgsmål til dig, hvad er kompensationsteoremet?