Et filter kan defineres, da det er en slags kredsløb, der bruges til at omforme, ændre og på anden måde afvise alle uønskede frekvenser i et signal. Et ideelt RC-filter opdeler og tillader overførsel af indgangssignaler (sinusformet) afhængigt af frekvensen. Generelt i lavfrekvens (<100 kHz) applications, passive filtre er konstrueret ved hjælp af modstands- og kondensatorkomponenter. Så det er kendt som en passivt RC-filter . På samme måde kan passive filtre til højfrekvente (> 100 kHz) signaler designes med modstand-induktorkondensatorkomponenter. Så disse kredsløb kaldes passive RLC kredsløb . Disse filtre kaldes så baseret på frekvensområdet for signalet, som de lader passere dem. Der er almindeligvis tre filterdesign, som f.eks lavpasfilter, højpasfilter og båndpasfilter . Denne artikel diskuterer en oversigt over lavpasfilteret.
Hvad er et lavpasfilter?
Det definition af lavpasfilter eller LPF er en slags filter, der bruges til at sende signaler med lav frekvens såvel som dæmpes med høj frekvens end en foretrukken afskæringsfrekvens. Det lavpasfilterfrekvensrespons afhænger hovedsageligt af Lav pas filter design . Disse filtre findes i flere former og giver den glattere type signal. Designerne bruger ofte disse filter som et prototype filter med impedans såvel som enhedsbåndbredde.
Det foretrukne filter erhverves fra prøven ved at afbalancere den foretrukne impedans og båndbredde og ændringer til den foretrukne båndtype som lavpas (LPF), højpas (HPF) , båndpas (BPSF) eller båndstop (BSF).
Første ordres lavpasfilter
En første ordens LPF er vist i figuren. Hvad er dette kredsløb? En simpel integrator. Bemærk, at integrator er den grundlæggende byggesten til LPF'er.

Første ordres lavpasfilter
Antage Z1 = 1 / 𝑗⍵𝐶1
V1 = Vi *𝑍1/𝑅1+𝑍1 = Vi (1/𝑗⍵𝐶1) / 𝑅1+(1 /𝑗⍵𝐶1)
= Vi 1/ 𝑗𝜔𝐶1𝑅1+1
= Vi 1/𝑠𝐶1𝑅1+1
Her s = j⍵
lavpasfilteroverføringsfunktion er
𝑉1/𝑉𝑖 =1 / 𝑠𝐶1𝑅1+1
Outputtet reducerer (dæmpes) omvendt som frekvensen. Hvis frekvens fordobles, er output halvdelen (-6 dB for hver fordobling af frekvensen ellers - 6 dB pr. Oktav). Dette er en LPF af første orden, og afviklingen er på -6 dB pr. Oktav.
Anden ordens lavpasfilter
Det Anden ordens lavpasfilter er vist i figuren.

Anden ordens lavpasfilter
Antage Z1 = 1 / 𝑗⍵𝐶1
V1 = Vi 𝑍1/𝑅1+𝑍1
Vi*(1/𝑗⍵𝐶1)/𝑅1+(1/𝑗⍵𝐶1)
Vi 1/ 𝑗𝜔𝐶1𝑅1+1
= Vi 1/𝑠𝐶1𝑅1+1
Her s = j⍵
Funktion til overførsel af lavpasfilter
𝑉1/𝑉𝑖 =1 / 𝑠𝐶1𝑅1+1
Antage Z2 = 1 / 𝑗⍵𝐶1
V1 = Vi 𝑍2/𝑅2+𝑍2
Vi * (1 / 𝑗⍵𝐶2) / 𝑅2 + (1 / 𝑗⍵𝐶2)
Vi 1 / 𝑗𝜔𝐶2𝑅2 + 1
= Vi 1/𝑠𝐶2𝑅2+1
Vi (1 / 𝑠𝐶1𝑅1+1)* (1/ 𝑠𝐶2𝑅2+1)
= 1 / (𝑠2𝑅1𝑅2𝐶1𝐶2 + 𝑠 (𝑅1𝐶1 + 𝑅2𝐶2) +1)
Derfor er overførselsfunktion en anden ordens ligning.
𝑉𝑜 / 𝑉𝑖 = 1 / (𝑠2𝑅1𝑅2𝐶1𝐶2 + 𝑠 (𝑅1𝐶1 + 𝑅2𝐶2) +1)
Output reducerer (dæmpes) omvendt som kvadratet af frekvensen. Hvis frekvens fordobles, er output cc / 4. (- 12 dB for hver fordobling af frekvens eller - 12 dB pr. Oktav). Dette er et lavpasfilter af anden orden, og rullen på er ved -12 dB pr. Oktav.
Det lavpasfilter bode plot er vist nedenfor. Generelt betegnes frekvensresponset for et lavpasfilter ved hjælp af et Bode-plot, og dette filter skelnes med sin afskæringsfrekvens såvel som frekvensen for afrulning
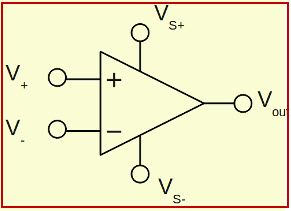
Lavpasfilter ved hjælp af opforstærker
Op-forstærkere eller operationelle forstærkere levere meget effektive lavpasfiltre uden brug af induktorer. Feedback-sløjfen for en op-amp kan inkorporeres med de grundlæggende elementer i et filter, så de højtydende LPF'er dannes let ved hjælp af de nødvendige komponenter undtagen induktorer. Det anvendelser af op-amp LPF'er anvendes i forskellige områder af strømforsyninger til output af DAC (digital til analog konvertere) til at fjerne alias-signaler såvel som andre applikationer.
Første ordens aktive LPF-kredsløb ved hjælp af Op-Amp
Det kredsløbsdiagram af enkeltpolen eller første ordre aktivt lavpasfilter er vist nedenfor. Kredsløbet til lavpasfilter ved hjælp af op-amp anvendelser en kondensator på tværs af feedbackmodstanden. Dette kredsløb har en effekt, når frekvensen øges for at forbedre feedbackniveauet, så falder kondensatorens reaktive impedans.

Første ordres lavpasfilter ved hjælp af op-forstærker
Beregningen af dette filter kan udføres ved at arbejde på den frekvens, hvormed kondensatorreaktansen kan svare til modstanden af modstanden. Dette kan opnås ved hjælp af følgende formel.
Xc = 1 / π f C
Hvor 'Xc' er den kapacitive reaktans i ohm
'Π' er standardbrevet, og værdien af dette er 3,412
'F' er frekvensen (enheder-Hz)
'C' er kapacitansen (Enheder-Farads)
In-band forstærkning af disse kredsløb kan beregnes på en enkel måde ved at eliminere kondensatorens effekt.
Da disse typer kredsløb er nyttige til at give en reduktion inden for forstærkning ved høje frekvenser, såvel som tilbyder en ultimativ hastighed til afrulning på 6 dB for hver oktav, hvilket betyder, at o / p-spændingen deler sig for hver gentagelse i frekvens. Så denne type filter er navngivet som første ordens eller enkeltpolet lavpasfilter.
Anden ordens aktive LPF-kredsløb ved hjælp af Op-Amp
Ved at bruge en operationel forstærker , er det muligt at designe filtre i en bred vifte med forskellige forstærkningsniveauer såvel som roll-off-modeller. Dette filter tilbyder både båndbreddesvar og enhedsgevinst.

Anden ordens aktive LPF-kredsløb ved hjælp af Op-Amp
Beregningerne af kredsløbsværdierne er ukomplicerede for svaret fra Butterworth lavpasfilter & enhed gevinst. Betydelig dæmpning er nødvendig for disse kredsløb & forholdsværdierne for kondensatoren og modstanden konkluderer dette.
R1 = R2
C1 = C2
f = 1 - √4 π R C2
Mens du vælger værdierne, skal du sørge for, at modstandens værdier falder i området mellem 10 kilo ohm til 100 kilo-ohm. Dette er umagen værd, da kredsløbets o / p-impedans øges med frekvensen og udvendige værdier i dette afsnit kan ændre handlingen.
Lavpasfilterberegner
Til en RC lavpasfilterkredsløb , det lavpasfilterberegner beregner delefrekvensen og plotter Graf for lavpasfilter som er kendt som et budskab plot.
For eksempel:
Lavpasfilteroverføringsfunktionen kan beregnes ved hjælp af følgende formel, hvis vi kender værdierne for modstanden og kondensatoren i kredsløbet.
Vout (er) / Vin (er) + 1 / CR / s + 1 / CR
Beregn frekvensværdien for den givne modstand samt kondensatorværdier
fc = 1/2 πRC

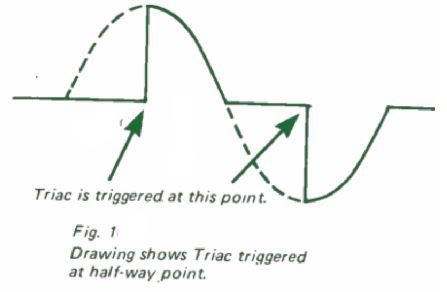
LPF bølgeform
Lavpasfilterapplikationer
Anvendelserne af lavpasfilter inkluderer følgende.
- Lavpasfiltre bruges i telefonsystemer til konvertering af lydfrekvenser i højttaleren til et båndbegrænset stemmebåndssignal.
- LPF'er bruges til at filtrere højfrekvent signal, der er kendt som 'støj' fra et kredsløb, da signalet føres gennem dette filter, så det meste af højfrekvenssignalet elimineres, såvel som en åbenbar støj kan produceres.
- Lavpasfilter ind billedbehandling til at forbedre billedet
- Nogle gange er disse filtre kendt som diskant eller høj cut på grund af applikationerne i lyd.
- Et lavpasfilter bruges i et RC-kredsløb, der er kendt som et RC lavpasfilter .
- LPF bruges som en integrator som et RC-kredsløb
- I multi-rate DSP, mens LP'en udføres, anvendes LPF som et Anti-Imaging Filter. Tilsvarende, når dette decimator udføres, bruges dette filter som et anti-aliasing-filter.
- Lavpasfiltre bruges i modtagere som super heterodyne til et effektivt svar på basisbåndsignalerne.
- Lavpasfilter bruges i signalerne fra medicinsk udstyr, der kommer fra menneskekroppen, mens test med elektroderne er mindre hyppigt. Så disse signaler kan strømme gennem LPF'en for at fjerne noget uønsket omgivende lyd.
- Disse filtre bruges til konvertering af arbejdscyklusamplitude såvel som fasedetektion i den faselåste sløjfe.
- LPF bruges i AM-radio til diodedetektoren til at ændre det AM-modulerede mellemfrekvenssignal til lydsignalet.
Dette handler altså om en lavpasfilter . Designet af op-amp-baseret LPF er let at designe såvel som mere komplicerede designs ved hjælp af forskellige typer filtre. Til flere applikationer leverer LPF en enestående præstation. Her er et spørgsmål til dig, hvad er lavpasfilterets hovedfunktion?