Sådan fungerer Buck-Boost-kredsløb

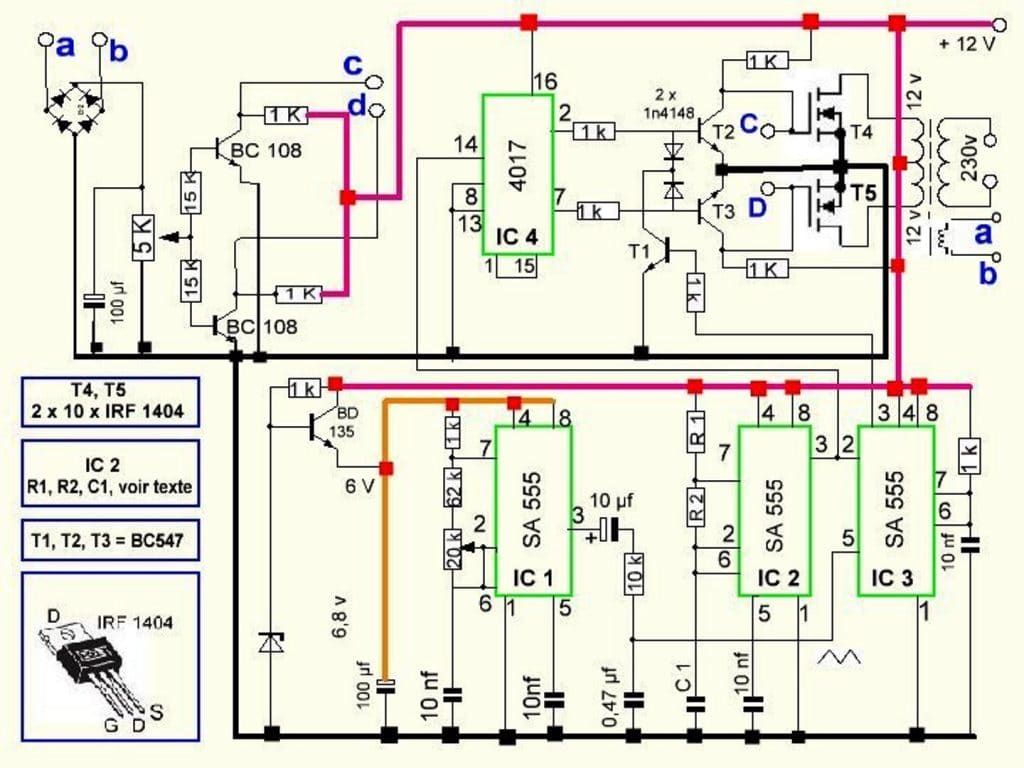
Vi har alle hørt meget om buck- og boost-kredsløb og ved, at disse kredsløb grundlæggende bruges i SMPS-design til at træde op eller ned på en given spænding ved indgangen. Det interessante ved denne teknologi er, at den tillader ovenstående funktioner med ubetydelig varmeproduktion, hvilket resulterer i en ekstremt effektiv konvertering.

Hvad er Buck-Boost, hvordan det fungerer

Lad os lære konceptet i det første afsnit uden at involvere meget tekniske, så det bliver lettere at forstå, hvad der præcist er boost-koncept, selv for en nybegynder.

Blandt de tre grundlæggende topologier med navnet buck, boost og buck-boost er den tredje mere populær, da det giver mulighed for at bruge begge funktionerne (buck boost) gennem en enkelt konfiguration bare ved at ændre inputimpulser.

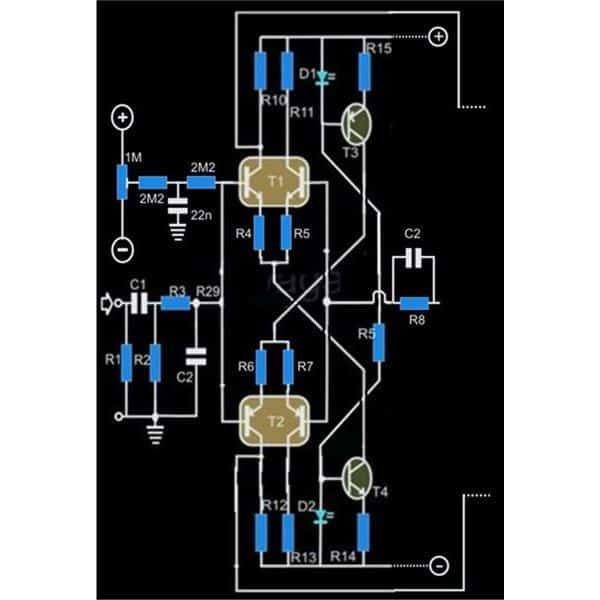
I top-boost-topologien har vi primært en elektronisk koblingskomponent, som kan være i form af en transistor eller en mosfet. Denne komponent skiftes via et pulserende signal fra et integreret oscillatorkredsløb.

Bortset fra ovenstående koblingskomponent har kredsløbet en induktor, en diode og en kondensator som hovedingredienser.

Alle disse dele er arrangeret i den form, der kan ses i følgende diagram:

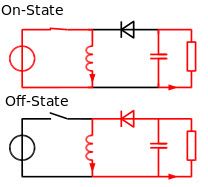
Med henvisning til ovenstående bog-boost-diagram er mosfet den del, der modtager impulser, der tvinger den til at fungere under to forhold: ON-tilstand og OFF-tilstand.

Under ON-tilstand får indgangsstrømmen en klar sti gennem mosfet og forsøger straks at komme igennem induktoren, da dioden er placeret i den omvendte forspændte tilstand.

Spolen på grund af dets iboende egenskab forsøger at begrænse den pludselige tilførsel af strøm og gemmer i et kompenserende svar en vis mængde strøm i den.

Så snart mosfet er slukket, går det i OFF-tilstand og blokerer enhver passage af indgangsstrømmen.

Igen er induktoren ikke i stand til at klare denne pludselige ændring af strøm fra en given størrelse til nul, og som et svar på at kompensere for dette sparker den sin lagrede strøm tilbage via dioden over udgangen af ​​kredsløbet.

I processen lagres strømmen også i kondensatoren.

Under den næste ON-tilstand af mosfet gentages cyklussen som ovenfor, men uden strøm tilgængelig fra induktoren, kondensatoren udleder den lagrede energi i output, hvilket hjælper med at holde output stabilt i den optimerede grad.

Du undrer dig måske over, hvilken faktor der bestemmer BUCK eller BOOST-resultaterne ved output? Det er ret simpelt, det afhænger af, hvor længe mosfet har lov til at forblive i ON-tilstand eller i OFF-tilstand.

Med en stigning i mosfets ON-tid begynder kredsløbet at blive omdannet til en Boost-konverter, mens mosfets OFF-tid overstiger sin ON-tid resulterer i, at kredsløbet opfører sig som en Buck-konverter.

Således kan input til mosfet foretages gennem et optimeret PWM-kredsløb til at få de krævede overgange over det samme kredsløb.

Udforskning af Buck / Boost Topology i SMPS-kredsløb mere teknisk:

Som diskuteret i ovenstående afsnit er de tre grundlæggende topologier, der populært bruges med switch mode strømforsyninger, buck, boost og buck boosts.

Disse er dybest set ikke-isolerede, hvor indgangseffektstrinet deler en fælles base med udgangseffektafsnittet. Selvfølgelig kunne vi også finde isolerede versioner, selvom de er ret sjældne.

Ovenstående udtrykte tre topologier kan skelnes entydigt afhængigt af deres eksklusive egenskaber. Egenskaberne kan identificeres som steady state spændingskonverteringsforhold, arten af ​​indgangs- og udgangsstrømmen og karakteren af ​​udgangsspændingsrippel også.

Derudover kan driftscyklusens frekvensrespons til udgangsspændingskørsel betragtes som en af ​​de vigtige egenskaber.

Blandt de ovennævnte tre topologier er buck-boost-topologi den mest foretrukne, fordi den tillader udgangen at arbejde spændinger mindre end indgangsspændingen (buck-tilstand) og også producere spændinger over indgangsspændingen (boost-tilstand).

Udgangsspændingen kan dog altid erhverves med den modsatte polaritet fra indgangen, hvilket ikke skaber nogen problemer overhovedet.

Den anvendte indgangsstrøm til en buck boost-konverter er form af en pulserende strøm på grund af omskiftningen af ​​den tilknyttede afbryder (Q1).

Her skifter strømmen fra nul til l under hver pulscyklus. Det samme gælder også for udgangen, og vi får en pulserende strøm på grund af den tilhørende diode, der kun leder i en retning, hvilket forårsager en TIL og FRA-pulserende situation under skiftecyklussen .

Kondensatoren er ansvarlig for at tilvejebringe kompenserende strøm, når dioden er i slukket eller omvendt forspændt tilstand under skiftecyklusser.

Denne artikel forklarer steady state-funktionaliteten af ​​buck-boost-konverteren i kontinuerlig tilstand og diskontinuerlig drift med eksempler på bølgeformer præsenteret.

Driftscyklus-til-udgangsspændingsudvekslingsfunktionaliteten præsenteres efter en introduktion af PWM-switchdesignet.

Figur 1 er et forenklet skema over buck-boost-effekttrin med tilføjet en drevkredsløbsblok. Afbryderen, Q1, er en n-kanal MOSFET. Udgangsdioden er CR1.

Spolen, L og kondensatoren, C, udgør den effektive outputfiltrering. Kondensatoren ESR, RC, (ækvivalent seriemodstand) og induktorens DC-modstand, RL, analyseres alle i. Modstanden, R, svarer til den belastning, der er identificeret ved effekttrinudgangen.

I løbet af regelmæssig funktionalitet i buck-boost-effektfasen tændes og slukkes Q1 konstant med tænd- og slukketiderne styret af kontrolkredsløbet.

Denne skifteadfærd tillader en kæde af impulser ved krydset mellem Q1, CR1 og L.

Selvom induktoren, L, er koblet til udgangskondensatoren, C, hvis kun CR1 leder, oprettes et vellykket L / C-udgangsfilter. Det renser rækkefølgen af ​​impulser for at resultere i en jævnstrømsudgangsspænding.

Buck-Boost Steady-State-analyse

Et effekttrin kan fungere i kontinuerlig eller diskontinuerlig induktorstrømindstilling. Kontinuerlig induktorstrømtilstand identificeres kontinuerligt med strøm i induktoren over skiftesekvensen i steady-state-proces.

Diskontinuerlig induktorstrømtilstand identificeres ved, at induktorstrømmen forbliver nul i et afsnit af skiftecyklussen. Det begynder ved nul, strækker sig til en maksimumsværdi og vender tilbage til nul i løbet af hvert skiftemønster.

De to forskellige metoder nævnes i meget større detaljer bagefter, og modelforslag til induktorværdien for at opretholde en valgt funktionalitet, da evnen til nominel belastning præsenteres. Det er temmelig fordelagtigt for en konverter at være i et enkelt format kun over sine forudsagte funktionsforhold, da effekttrinfrekvensresponset ændrer sig væsentligt mellem de to forskellige driftsteknikker.

Med denne vurdering anvendes en n-kanal effekt MOSFET, og en positiv spænding, VGS (ON), leveres fra porten til kileterminalerne i Q1 af styrekredsløbet for at tænde FET. Fordelen ved at anvende en n-kanal FET er dens lavere RDS (on), men kontrakredsløbet er vanskeligt, fordi et suspenderet drev bliver nødvendigt. For de identiske pakkedimensioner har en p-kanal FET en højere RDS (til), men det er typisk ikke nødvendigvis nødvendigt med et flydende drevkredsløb.

Transistoren Q1 og dioden CR1 er illustreret inde i en stiplet linie med terminaler mærket a, p og c. Det diskuteres grundigt i delen Buck-Boost Power Stage Modelling.

Buck-Boost Steady-state kontinuerlig ledningsmetode analyse

Det følgende er en beskrivelse af buck boost-arbejde i steady-state-drift i kontinuerlig ledningsmetode. Det primære mål for dette segment ville være at præsentere en afledning af spændingstransformationsforholdet for det kontinuerlige ledningstilstand buck-boost power-trin.

Dette vil være vigtigt, da det angiver den måde, hvorpå udgangsspændingen bestemmes af driftscyklus og indgangsspænding eller tværtimod, hvordan driftscyklus kunne bestemmes afhængigt af indgangsspænding og udgangsspænding.

Steady-state betyder, at indgangsspænding, udgangsspænding, udgangsbelastningsstrøm og driftscyklus er konstant i modsætning til varierende. Store bogstaver leveres normalt til variable etiketter for at antyde en steady-state størrelse. I kontinuerlig ledningstilstand tager buck-boost-konverteren et par tilstande pr. Skiftecyklus.

ON-tilstanden er hver gang Q1 er ON, og CR1 er OFF. OFF-tilstanden er hver gang Q1 er OFF, og CR1 er ON. Et let lineært kredsløb kunne symbolisere hver af de to tilstande, hvor omskifterne i kredsløbet erstattes af deres matchende kredsløb i løbet af hver tilstand. Kredsløbsdiagrammet for hver af de to betingelser er vist i figur 2.

Perioden for ON-tilstand er D × TS = TON, hvor D er driftscyklus, fastgjort af drivkredsløbet, afbildet i form af et forhold mellem switch ON-perioden og perioden for en enkelt fuld koblingssekvens, Ts.

Længden af ​​OFF-tilstanden er kendt som TOFF. Fordi man kun kan finde et par betingelser pr. Skiftecyklus til kontinuerlig ledningstilstand, er TOFF lig med (1 − D) × TS. Størrelsen (1 − D) kaldes lejlighedsvis D ’. Disse perioder er præsenteret sammen med bølgeformerne i figur 3.

Ser man på figur 2, i løbet af ON-tilstanden, tilbyder Q1 en reduceret modstand, RDS (til), fra dens afløb til kilde og manifesterer et mindre spændingsfald på VDS = IL × RDS (til).

Derudover er der et lille spændingsfald over induktorens DC-modstand svarende til IL × RL.

Derved sættes indgangsspændingen, VI, minus underskud, (VDS + IL × RL) på tværs af induktoren, L. CR1 er OFF inden for denne periode, da den ville være omvendt forspændt.

Induktorstrømmen, IL, passerer fra indgangsforsyningen, VI, ved hjælp af Q1 og til jord. I løbet af ON-tilstanden er spændingen på induktoren konstant og den samme som VI - VDS - IL × RL.

Efter polaritetsnormen for den nuværende IL, der er vist i figur 2, øges induktorstrømmen på grund af den udførte spænding. Desuden, fordi den anvendte spænding er grundlæggende konsistent, stiger induktorstrømmen lineært. Denne boost i induktorstrøm i løbet af TON er trukket ud i figur 3.

Niveauet, hvormed induktorstrømmen øges, bestemmes generelt ved anvendelse af en form med den velkendte formel:

Induktorens nuværende stigning i løbet af ON-status præsenteres som:

Denne størrelse, ΔIL (+), kaldes induktorens krusningsstrøm. Yderligere bemærkes, at gennem dette interval kommer hver bit af udgangsbelastningsstrømmen ind af udgangskondensatoren, C.

Med henvisning til figur 2, mens Q1 er OFF, tilbyder den en øget impedans fra dens afløb til kilde.

Derfor skifter strømmen fra Q1 til CR1, fordi strømmen, der kører i induktoren L, ikke kan justeres med det samme. Som et resultat af den reducerende induktorstrøm vender spændingen over induktoren polariteten, indtil ensretter CR1 bliver forspændt fremad og vender TIL.

Spændingen forbundet over L bliver til (VO - Vd - IL × RL), hvor størrelsen, Vd, er det fremadrettede spændingsfald på CR1. Induktorstrømmen, IL, passerer på dette tidspunkt fra udgangskondensatoren og belastningsmodstandsarrangementet via CR1 og til den negative linje.

Vær opmærksom på, at justeringen af ​​CR1 og strømcirkulationsstien i induktoren betyder, at strømmen, der kører i udgangskondensatoren og belastningsmodstandsgruppering, fører til, at VO er minus spænding. I løbet af OFF-tilstanden er spændingen forbundet over induktoren stabil og den samme som (VO - Vd - IL × RL).

Ved at bevare vores ligeledes polaritetskonvention er denne tilsluttede spænding minus (eller omvendt i polaritet fra den tilsluttede spænding i løbet af ON-tiden) på grund af det faktum, at udgangsspændingen VO er negativ.

Derfor sænkes induktorstrømmen gennem hele OFF-tiden. Desuden reduceres induktorstrømmen lineært, fordi den tilsluttede spænding dybest set er stabil. Denne reduktion i induktorstrøm i løbet af TOFF er beskrevet i figur 3.

Induktorens strømreduktion gennem OFF-situationen leveres af:

Denne størrelse, ΔIL (-), kan betegnes induktorens krusningsstrøm. I situationer med stabil tilstand skal strømstigningen ΔIL (+) i løbet af ON-tiden og strømreduktionen gennem OFF-tiden, ΔIL (-) være identisk.

Ellers kunne induktorstrømmen tilbyde en samlet boost eller reduktion fra cyklus til cyklus, der ikke ville være en stabil tilstandsforhold.

Således kan begge disse ligninger sidestilles med og udarbejdes for VO til at erhverve den kontinuerlige ledning fra buck-boost spændingsændringstilknytning:

Bestemmelse for VO:

Ud over at erstatte TS for TON + TOFF og anvende D = TON / TS og (1 − D) = TOFF / TS, er ligningstilstandsligningen for VO:

Vær opmærksom på, at TON + TOFF formodes at ligne TS ved forenkling af ovenstående. Dette kan kun være ægte for kontinuerlig ledningstilstand, som vi vil opdage i den diskontinuerlige ledningstilstandsevaluering. En vigtig kontrol bør foretages på dette tidspunkt:

Fastsættelse af de to værdier af ΔIL på niveau med hinanden er nøjagtigt lig med at udjævne volt-sekunder på induktoren. De anvendte volt-sekunder på induktoren er produktet af den anvendte spænding og den periode, hvor spændingen anvendes.

Dette kan være den mest effektive måde at estimere uidentificerede størrelser på for eksempel VO eller D med hensyn til fælles kredsløbsparametre, og denne tilgang vil blive brugt ofte i denne artikel. Volt-sekund stabilisering på induktoren er et naturligt krav og burde opfattes i det mindste yderligere som Ohms Law.

I ovenstående ligninger for ΔIL (+) og ΔIL (-) skulle udgangsspændingen implicit være konsistent uden AC-krusningsspænding i hele ON-tiden og OFF-perioden.

Dette er en accepteret forenkling og medfører et par individuelle resultater. For det første menes det, at udgangskondensatoren er tilstrækkelig stor, så dens spændingskonvertering er minimal.

For det andet anses spændingen, som kondensatoren ESR desuden er for minimal. Sådanne antagelser er legitime, da AC-rippelspændingen helt sikkert vil være signifikant lavere end DC-delen af ​​output-spændingen.

Ovenstående spændingsændring for VO demonstrerer sandheden om, at VO kunne justeres ved finjustering af driftscyklus, D.

Denne forbindelse nærmer sig nul, når D ankommer nær nul og stiger uden bestemmelse, når D nærmer sig 1. En typisk forenkling overvejer VDS, Vd og RL er små nok til at forsømme. Opretter VDS, Vd og RL til nul, den ovenstående formel forenkler mærkbart til:

En mindre kompliceret, kvalitativ metode til at afbilde kredsløbets drift ville være at betragte induktoren som en strømlagringsdel. Hver gang Q1 er tændt, hældes energi over induktoren.

Mens Q1 er slukket, forsyner induktoren en del af sin energi tilbage til udgangskondensatoren og belastningen. Udgangsspændingen reguleres ved at fastlægge on-time for Q1. For eksempel forstærkes mængden af ​​effekt, der sendes til induktoren, ved at hæve tiden på Q1.

Yderligere energi sendes efterfølgende til udgangen i løbet af off-time for Q1, hvilket forårsager en stigning i udgangsspændingen. I modsætning til bukkeffektstrinnet er den typiske størrelse af induktorstrømmen ikke den samme som udgangsstrømmen.

For at knytte induktorstrømmen til udgangsstrømmen, se på figur 2 og 3, skal du observere, at induktorstrømmen til udgangen udelukkende er, når den er i slukket tilstand for strømtrinet.

Denne gennemsnitlige strøm over en hel koblingssekvens er den samme som udgangsstrømmen, da den omtrentlige strøm i udgangskondensatoren skal svare til nul.

Forbindelsen mellem den gennemsnitlige induktorstrøm og udgangsstrømmen for den kontinuerlige tilstand buck-boost effektstrin tilvejebringes af:

Et andet væsentligt synspunkt er, at den typiske induktorstrøm er proportional med udgangsstrømmen, og fordi induktorens krusningsstrøm, ΔIL, ikke er relateret til udgangsbelastningsstrømmen, følger de minimale og de højeste værdier af induktorstrømmen den gennemsnitlige induktorstrøm nøjagtigt.

Som et eksempel, hvis den gennemsnitlige induktorstrøm falder med 2A på grund af en belastningsstrømreduktion, reduceres i så fald de laveste og højeste værdier af induktorstrømmen med 2A (i betragtning af kontinuerlig ledningstilstand bevares).

Den foregående evaluering var for funktionaliteten til buck-boost power stage i kontinuerlig induktorstrømtilstand. Det følgende segment er en forklaring på steady-state funktionalitet i diskontinuerlig ledningstilstand. Det primære resultat er en afledning af spændingsomdannelsesforholdet for det diskontinuerlige ledningstilstand buck-boost power-trin.

Buck-Boost Steady-state diskontinuerlig ledningsevaluering

Vi undersøger på dette tidspunkt, hvad der sker, hvor belastningsstrømmen reduceres, og ledningstilstanden skifter fra kontinuerlig til diskontinuerlig.

Husk for kontinuerlig ledningstilstand, at den gennemsnitlige induktorstrøm sporer udgangsstrømmen, dvs. hvis udgangsstrømmen reduceres, i så fald vil den gennemsnitlige induktorstrøm også.

Desuden forfølger de laveste og højeste toppe af induktorstrømmen den gennemsnitlige induktorstrøm nøjagtigt. Hvis udgangsbelastningsstrømmen falder til under det grundlæggende strømniveau, ville induktorstrømmen være nul for en del af skiftesekvensen.

Dette ville være tydeligt af bølgeformerne præsenteret i figur 3, fordi top til top-niveauet af krusningsstrømmen ikke er i stand til at ændre sig med outputbelastningsstrømmen.

Hvis en induktorstrøm forsøger at være under nul, stopper den simpelthen ved nul (på grund af den ensrettet strømbevægelse i CR1) og fortsætter der indtil starten af ​​den efterfølgende skiftehandling. Denne arbejdstilstand er kendt som diskontinuerlig ledningstilstand.

Et power stage-arbejde af buck boost-kredsløb i diskontinuerligt ledningsformat har tre karakteristiske tilstande gennem hver skiftecyklus i modsætning til 2 tilstande for kontinuerligt ledningsformat.

Induktorens nuværende tilstand, hvor effekttrinet er i periferien mellem kontinuerlig og diskontinuerlig indstilling, er vist i figur 4.

I dette kollapser induktorstrømmen simpelthen til nul, mens den følgende skiftecyklus begynder lige efter at strømmen når nul. Vær opmærksom på, at værdierne af IO og IO (Crit) er anført i figur 4, da IO og IL inkluderer modsatrettede polariteter.

Længere sænkning af outputbelastningsstrøm sætter effekttrinet i diskontinuerligt ledningsmønster. Denne betingelse er tegnet i figur 5.

Den diskontinuerlige tilstandseffektfrekvensrespons er ret forskellig fra det kontinuerlige tilstands frekvensrespons, som præsenteres i Buck-Boost Power Stage Modeling-segmentet. Derudover er input til output-forbindelsen temmelig forskellig som vist på denne sideafledning:

For at starte afledningen af ​​det diskontinuerlige ledningstilstand buck-boost power stage spændingsændringsforhold skal du huske at du har tre karakteristiske tilstande, som konverteren overvejer gennem diskontinuerlig ledningstilstandsfunktionalitet.

ON-tilstanden er, når Q1 er ON, og CR1 er OFF. OFF-tilstanden er, når Q1 er OFF, og CR1 er ON. IDLE-tilstanden er, når hver Q1 og CR1 er OFF. De to indledende betingelser ligner meget den kontinuerlige tilstandssituation, og kredsløbene i figur 2 er relevante bortset fra den TOFF ≠ (1 − D) × TS. Resten af ​​skiftesekvensen er IDLE-tilstanden.

Derudover formodes udgangsspolens DC-modstand, fremadspændingsfaldets spændingsfald såvel som spændingsfaldet MOSFET ON-state normalt at være minut nok til at overse.

Tidsperioden for ON-tilstanden er TON = D × TS, hvor D er driftscyklussen, fastgjort af styrekredsløbet, angivet som et forhold mellem tændtiden og tiden for en fuld koblingssekvens, Ts. Længden af ​​OFF-tilstand er TOFF = D2 × TS. IDLE-perioden er resten af ​​skiftemønsteret, der præsenteres som TS - TON - TOFF = D3 × TS. Disse perioder er sat op med bølgeformerne i figur 6.

Uden at kontrollere den omfattende beskrivelse er ligningerne for induktorens aktuelle stigning og fald opregnet nedenfor. Induktorens nuværende stigning i løbet af ON-tilstanden udstedes af:

Rippelstrømsmængden, ΔIL (+), er ligeledes den maksimale induktorstrøm, Ipk, da i diskontinuerlig tilstand begynder strømmen ved 0 hver cyklus. Induktorstrømreduktionen i løbet af OFF-tilstand præsenteres af:

Ligesom situationen med kontinuerlig ledningstilstand er den aktuelle stigning, ΔIL (+), i løbet af ON-tiden og den aktuelle reduktion, mens den er i OFF-tiden, ΔIL (-), identisk. Således kunne begge disse ligninger sidestilles med og adresseres til VO for at erhverve initialen af ​​to ligninger, der skal bruges til at løse spændingskonverteringsforholdet:

Dernæst bestemmer vi udgangsstrømmen (udgangsspændingen VO divideret med udgangsbelastningen R). Det er gennemsnittet over en koblingssekvens af induktorstrømmen på det tidspunkt, hvor CR1 bliver ledende (D2 × TS).

Her skal du udskifte forbindelsen til IPK (ΔIL (+)) i ovenstående ligning for at erhverve:

Derfor har vi to ligninger, den ene for udgangsstrømmen (VO divideret med R), der netop er afledt, og den ene for udgangsspændingen, begge med hensyn til VI, D og D2. Vi løfter på dette tidspunkt hver formel for D2 samt retter de to ligninger på niveau med hinanden.

Ved hjælp af den resulterende ligning kunne der anskaffes en illustration til udgangsspændingen, VO. Den diskontinuerlige ledningstilstand buck-boost spændingstransformationstilknytning er skrevet af:

Ovenstående forbindelse viser en af ​​de vigtigste forskelle mellem de to ledningstilstande. For diskontinuerlig ledningstilstand er spændingsændringsforholdet en funktion af indgangsspændingen, driftscyklus, effekttrinsinduktans, omskiftningsfrekvensen og udgangsbelastningsmodstanden.

For kontinuerlig ledningstilstand er spændingsændringsforbindelsen kun påvirket af indgangsspændingen og driftscyklussen. I traditionelle applikationer køres buck-boost power-trinnet i et valg mellem kontinuerlig ledningstilstand eller diskontinuerlig ledningstilstand. Til en bestemt anvendelse vælges en ledningstilstand, mens effektstrinet blev lavet for at opretholde den samme tilstand.