Matematik spiller en afgørende rolle for at forstå adfærd og arbejde med elektrisk og elektroniske systemer . Polynomer, algebra, sandsynlighed, integrationer og differentieringer osv ... udgør en væsentlig del af de værktøjer, der bruges til at løse systemerne. Med den stigende kompleksitet af systemer kræves meget sofistikerede metoder. Differentialligninger bruges fremtrædende til at definere kontrolsystemer. Disse ligninger er enkle at løse. Men kompleksitet opstår, når man løser differentialligninger med højere ordre. For at løse sådanne komplekse differentierede ligninger med højere ordre er den matematiske metode, der viste sig at være effektiv Laplace Transform . Da denne transformation er meget anvendt, er det nyttigt at vide, hvad de virkelig betød for, og hvordan fungerer de.
Hvad er en Laplace Transform?
I matematik anvendes transformer til at transformere en variabel fra en form til en anden for at gøre ligningen let at håndtere. Laplace transformerer stort set det samme. De omdanner højere ordens differentialligning til en polynomform, som er langt let end at løse differentialligning direkte.
Men der er forskellige transformationer som Fourier-transformer, z transformerer, hvad der gør Laplace-transformationen speciel? Den største fordel ved Laplace-transformation er, at de er defineret for både stabile og ustabile systemer, mens Fourier-transformationer kun er defineret for stabile systemer.
Laplace Transform Formula
En Laplace-transformation af funktion f (t) i et tidsdomæne, hvor t er det reelle tal større end eller lig med nul, gives som F (s), hvor der  s er det komplekse tal i frekvensdomæne, dvs. s = σ + jω
s er det komplekse tal i frekvensdomæne, dvs. s = σ + jω
Ovenstående ligning betragtes som ensidig Laplace transform ligning . Når grænserne udvides til hele den virkelige akse, så Bilateral Laplace-transformation kan defineres som
 I praktiske kredsløb som RC og RL kredsløb normalt anvendes indledende betingelser, så ensidige Laplace-transformer anvendes til analyseformål.
I praktiske kredsløb som RC og RL kredsløb normalt anvendes indledende betingelser, så ensidige Laplace-transformer anvendes til analyseformål.
Som s = σ + jω, når σ = 0 Laplace-transformerer opfører sig som Fourier-transformation.

Laplace Transform Formler
Betingelser for anvendelse af Laplace-transformation
Laplace-transformationer kaldes integrale transformationer, så der er nødvendige betingelser for konvergens af disse transformationer.
 dvs. f skal være lokalt integrerbar i intervallet [0, ∞) og afhængigt af, om σ er positiv eller negativ, kan e ^ (- σt) være ved at henfalde eller vokse. For bilaterale Laplace-transformationer snarere end en enkelt værdi konvergerer integralet over et bestemt interval af værdier kendt som Region of Convergence.
dvs. f skal være lokalt integrerbar i intervallet [0, ∞) og afhængigt af, om σ er positiv eller negativ, kan e ^ (- σt) være ved at henfalde eller vokse. For bilaterale Laplace-transformationer snarere end en enkelt værdi konvergerer integralet over et bestemt interval af værdier kendt som Region of Convergence.
Egenskaber ved Laplace Transform:
Lineæritet

Lineæritet
Time Shifting

Time Shifting
Skift i S-domæne

Skift i S-domæne
Tidsvending

Tidsvending
Differentiering i S-domæne

Differentiering i S-domæne
Convolution in Time

Convolution in Time
Initial Value Theorem
Startværdisætningen anvendes, når tælleren i Laplace-transform er mindre end graden af nævneren  Endelig værdi sætning:
Endelig værdi sætning:
Hvis alle polerne i sF (s) ligger i den venstre halvdel af S-planets endelige værdi sætning anvendes.
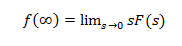 Omvendt laplace-transformation
Omvendt laplace-transformation
På grund af konvergens har Laplace-transformation også en omvendt transformation. Laplace-transformationer viser en-til-en-kortlægning fra et funktionsrum til et andet. Formlen for omvendt laplace-transformation er
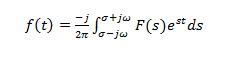 Hvordan man beregner Laplace Transform?
Hvordan man beregner Laplace Transform?
Laplace-transformation gør ligningerne lettere at håndtere. Når en højere ordens differentialligning er givet, anvendes Laplace-transformation til den, der konverterer ligningen til en algebraisk ligning, hvilket gør det lettere at håndtere. Derefter beregner vi rødderne ved forenkling af denne algebraiske ligning. Nu findes invers Laplace-transformation af enklere udtryk, der løser den givne højere ordens differentialligning.

Beregning af Laplace Transform
Anvendelser af Laplace Transform
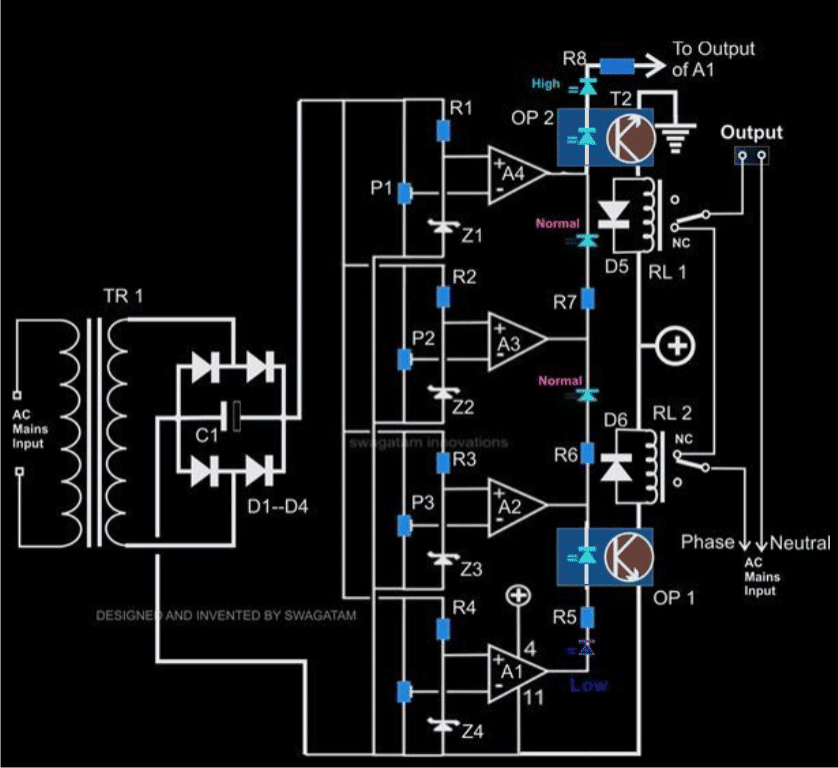
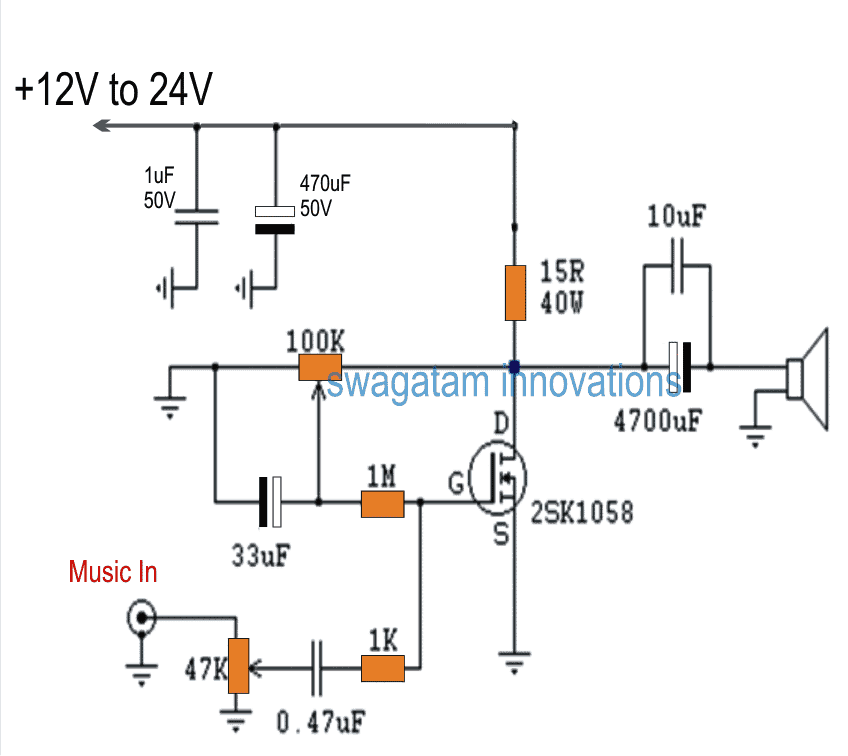
- Analyse af elektrisk og elektroniske kredsløb .
- Nedbrydning af komplekse differentialligninger i enklere polynomiske former.
- Laplace-transformation giver information om såvel stabile som forbigående tilstande.
- I maskinindlæring bruges Laplace-transformen til at foretage forudsigelser og foretage analyse i datamining.
- Laplace-transformation forenkler beregninger i systemmodellering.
Anvendelse af Laplace-transformation i signalbehandling
Laplace-transformationer vælges ofte til signalbehandling. Sammen med Fourier-transformationen er Laplace-transformation bruges til at studere signaler i frekvensdomænet. Når der er små frekvenser i signalet i frekvensdomænet, kan man forvente, at signalet er glat i tidsdomænet. Filtrering af et signal udføres normalt i frekvensdomænet, for hvilket Laplace fungerer som et vigtigt redskab til at konvertere et signal fra tidsdomæne til frekvensdomæne.
Anvendelse af Laplace Transform i kontrolsystemer
Kontrolsystemer er normalt designet til at kontrollere adfærd fra andre enheder. Eksempel på kontrolsystemer kan variere fra en simpel hjemmevarmestyring til et industrielt kontrolsystem, der regulerer maskiners opførsel.
Generelt bruger kontrolingeniører differentialligninger til at beskrive adfærden for forskellige lukkede sløjfefunktionelle blokke. Laplace-transform bruges her til at løse disse ligninger uden tab af vigtig variabel information.
Karakterisering af lineære tidsvariante systemer ved hjælp af Laplace-transformation
For et afslappet system-ROC, der er knyttet til systemet, er funktionen det højre halvplan. Et system er anti-afslappet, hvis dets impulsrespons h (t) = 0 for t> 0.
Hvis ROC i systemfunktionerne H (s) inkluderer jω-aksen, er L.T.I. systemet kaldes et stabilt system. Hvis et afslappet system med rationelle systemfunktioner H (s) har negative reelle dele for alle dets poler, er systemet stabilt.
Således er Laplace-transformation et afgørende værktøj til analyse af kredsløb. Vi kan sige, som et stetoskop er at læge Laplace transformerer er at kontrollere ingeniør. Hvad betragter du Laplace-transformationer som? På hvilken måde var de nyttige for dig?
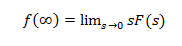 Omvendt laplace-transformation
Omvendt laplace-transformation 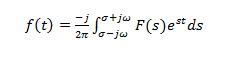 Hvordan man beregner Laplace Transform?
Hvordan man beregner Laplace Transform?