Den enkle harmoniske bevægelse blev opfundet af den franske matematiker Baron Jean Baptiste Joseph Fourier i 1822. Edwin Armstrong (18. DEC 1890 til 1. FEB 1954) observerede svingninger i 1992 i deres eksperimenter, og Alexander Meissner (14. SEP 1883 til 3. JAN 1958) opfandt oscillatorer i marts 1993. Udtrykket harmonisk er et latinsk ord. Denne artikel diskuterer en oversigt over den harmoniske oscillator, som inkluderer dens definition, type og dens anvendelser.

Hvad er harmonisk oscillator?

Harmonisk oscillator defineres som en bevægelse, hvor kraften er direkte proportional med partiklen fra ligevægtspunktet, og den producerer output i en sinusformet bølgeform. Kraften, der forårsager harmonisk bevægelse kan matematisk udtrykkes som

F = -Kx

Hvor,

F = Gendannelseskraft

K = Fjederkonstant

X = afstand fra ligevægt

blokdiagram-af-harmonisk-oscillator

Der er et punkt i harmonisk bevægelse, hvor systemet oscillerer, og den kraft, der bringer massen igen og igen på det samme punkt, hvorfra den starter, kaldes kraften gendannelseskraft, og punktet kaldes ligevægtspunkt eller middelposition. Denne oscillator er også kendt som en lineær harmonisk oscillator . Energien strømmer fra aktiv komponenter til passive komponenter i oscillatoren.

Blokdiagram

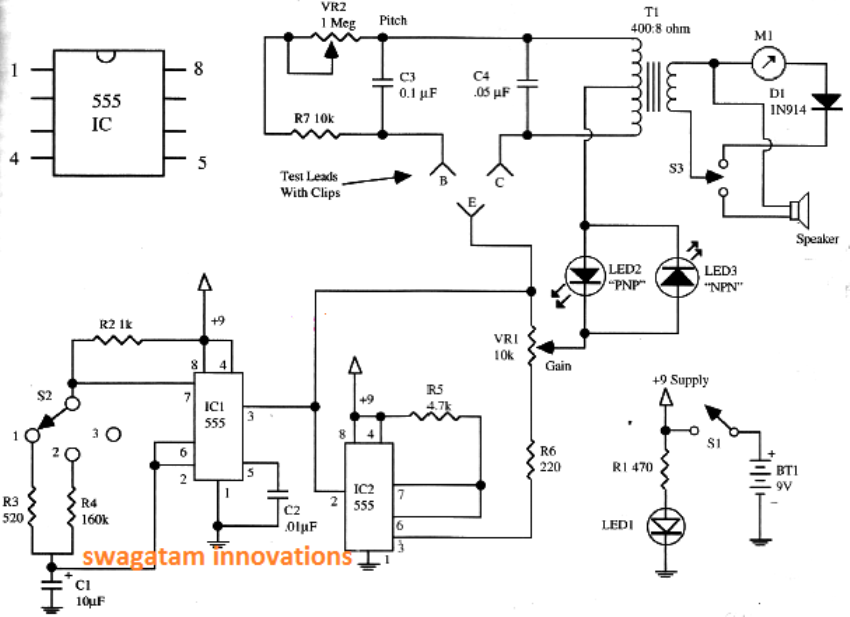
Det blokdiagram over den harmoniske oscillator består af en forstærker og et feedback-netværk. Forstærkeren bruges til at forstærke signalerne, og at forstærkede signaler føres gennem et feedbacknetværk og genererer output. Hvor Vi er indgangsspændingen, Vo er udgangsspændingen, og Vf er feedback-spændingen.

Eksempel

Masse på en forår: Fjederen tilvejebringer gendannelseskraft, der accelererer massen, og gendannelseskraften udtrykkes som

F = ma

Hvor 'm' er massen og a er en acceleration.

“hvordan man bygger en mikrokontroller ”

mass-on-a-spring

Foråret består af en masse (m) og kraft (F). Når kraften trækker massen i et punkt x = 0 og kun afhænger af x - massens position, og fjederkonstanten er repræsenteret af en bogstav k.

Typer af harmonisk oscillator

Typer af denne oscillator inkluderer primært følgende.

Tvungen harmonisk oscillator

Når vi anvender ekstern kraft til systemets bevægelse, siges bevægelsen at være en tvungen harmonisk oscillator.

Dæmpet harmonisk oscillator

Denne oscillator er defineret som, når vi anvender ekstern kraft til systemet, reduceres oscillatorens bevægelse, og dens bevægelse siges at være dæmpet harmonisk bevægelse. Der er tre typer dæmpede harmoniske oscillatorer, de er

dæmpning-bølgeformer

Over dæmpet

Når systemet bevæger sig langsomt mod ligevægtspunktet, siges det at være en overdampet harmonisk oscillator.

Under dæmpet

Når systemet bevæger sig hurtigt mod ligevægtspunktet, siges det at være en overdampet harmonisk oscillator.

Kritisk dæmpet

Når systemet bevæger sig hurtigt som muligt uden at svinge omkring ligevægtspunktet, siges det at være en overdampet harmonisk oscillator.

Kvantum

Det er opfundet af Max Born, Werner Heisenberg og Wolfgang Pauli ved “University of Göttingen”. Ordet kvante er det latinske ord, og betydningen af kvante er en lille mængde energi.

Zero Point Energy

Nulpunktenergien er også kendt som jordtilstandsenergi. Det defineres, når jordtilstandsenergi altid er større end nul, og dette koncept opdages af Max Planck i Tyskland og formlen udviklet i 1990.

Gennemsnitlig energi ved dæmpet simpel harmonisk oscillatorligning

Der er to typer energier, de er kinetisk energi og potentiel energi. Summen af kinetisk energi og potentiel energi er lig med den samlede energi.

E = K + U ………………. Ligestilling (1)

Hvor E = Total energi

K = Kinetisk energi

U = Potentiel energi

Hvor k = k = 1/2 mv^to………… ækv. (2)

U = 1/2 kx^to………… ækv. (3)

oscillationscyklus- for gennemsnitsværdier

De gennemsnitlige værdier for kinetisk og potentiel energi pr. Svingningscyklus er lig med

Hvor v^to= v^to(TIL^to-x^to) ……. ligning (4)

Stedfortræder eq (4) i eq (2) og eq (3) får

k = 1/2 m [w^to(TIL^to-x^to)]

= 1/2 m [Aw cos (wt + ø₀)]^to……. ligning (5)

U = 1/2 kx^to

= 1/2 k [A sin (wt + ø₀)]^to……. ækv. (6)

Erstatning af ækv. (5) og ækv. (6) i ækv. (1) får den samlede energiværdi

E = 1/2 m [w^to(TIL^to-x^to)] + 1/2 kx^to

= 1/2 m w^to-1/2 m w^toTIL^to+ 1/2 kx^to

= 1/2 m w^toTIL^to+1/2 x^to(K-mw^to) ……. ækv. (7)

Hvor mw^to= K , erstat denne værdi i ækv. (7)

E = 1/2 K A^to- 1/2 Kx^to+ 1/2 x^to= 1/2 K A^to

Samlet energi (E) = 1/2 K A^to

Gennemsnitlige energier for en tidsperiode udtrykkes som

TIL_gns= U_gns= 1/2 (1/2 K A^to)

Harmonisk oscillatorbølgefunktion

Hamilton-operatøren udtrykkes som en sum af kinetisk energi og potentiel energi, og den udtrykkes som

ђ (Q) = T + V ……………… .eq (1)

Hvor ђ = hamitonske operatør

T = Kinetisk energi

V = Potentiel energi

For at generere bølgefunktionen skal vi kende Schrodinger-ligningen, og ligningen udtrykkes som

-đ^to/ 2μ * d^toѱ_υ(Q) / dQ^to+ 1 / 2KQ^toѱ_υ(Q) = E_υѱ_υ(Q) …………. ækv. (2)

Hvor Q = den normale koordinats længde

Μ = Effektiv masse

K = Kraftkonstant

Schrodinger ligningsgrænsebetingelser er:

Ѱ (-∞) = ø

Ѱ (+ ∞) = 0

Vi kan også skrive eq (2) som

d^toѱ_υ(Q) / dQ^to+ 2μ / đ^to(E_υ-K / 2 * Q^to) ѱ_υ(Q) = 0 ………… ækv. (3)

Parametre, der bruges til at løse en ligning er

β = ђ / √μk ……… .. ækv. (4)

d^to/ dQ^to= 1 / β^tod^to/ dx^to………… .. ækv. (5)

Erstat eq (4) og eq (5) i eq (3), så bliver differentialligningen for denne oscillator

d^toѱ_υ(Q) / dx^to+ (2μb^toE_υ/ đ^to- x^to) ѱ_υ(x) = 0 ……… .. ækv. (6)

Det generelle udtryk for magtserier er

ΣC¬nx2 …………. ækv. (7)

En eksponentiel funktion udtrykkes som

exp (-x^to/ 2) ………… ækv. (8)

eq (7) ganges med eq (8)

ѱυ (x) = ΣC¬nx2exp (-x2 / 2) …………… ..ekv. (9)

Hermite-polynomer opnås ved hjælp af nedenstående ligning

ђ_υ(x) = (-1)^υ* exp (x^to) d / dx^υ* exp (-x^to) …………… .. ækv. (10)

Normaliseringskonstanten udtrykkes som

N_υ= (1/2^υυ! √Π)^1/2…………… .eq (11)

Det enkel harmonisk oscillatorløsning udtrykkes som

Ѱ_υ(x) = N_υH_υ(og) e^{-x2 / 2}……………… ækv. (12)

Hvor N_υer normaliseringskonstanten

H _υer eremiten

er ^{-x2 / to}er Gaussian

En ligning (12) er den harmoniske oscillators bølgefunktion.

Denne tabel viser det første udtryk Hermite polynomer for de laveste energitilstande

^υ	0	1	to	3
H_υ(Y)	1	2y	4y^to-to	8 år³-12 år

Bølgefunktionerne i enkel harmonisk oscillatorgraf for fire laveste energitilstande er vist i nedenstående figurer.

bølgefunktioner-af-harmonisk-oscillator

Sandsynlighedstæthederne for denne oscillator for de fire laveste energitilstande er vist i nedenstående figurer.

sandsynlighed -densiteter-af-bølgeformer

sandsynlighedsdensiteter-af-bølgeformer

Ansøgninger

Simple harmonisk oscillatorapplikationer inkluderer hovedsageligt følgende

Audio- og videosystemer
Radio og andre kommunikationsenheder
Omformere , Alarmer
Summere
Dekorative lys

Fordele

Det fordelene ved den harmoniske oscillator er

Billig
Højfrekvent generation
Høj effektivitet
Billig
Transportabel
Økonomisk

Eksempler

Eksemplet på denne oscillator inkluderer følgende.

Musikinstrumenter
Simpelt pendul
Massefjedersystem
Svinge
Bevægelsen fra urets hænder
Bevægelsen af hjulene på biler, lastbiler, busser osv

Det er en type bevægelse, som vi kan observere på vores daglige baser. Harmonisk oscillator bølgefunktion ved hjælp af Schrodinger og ligninger af den harmoniske oscillator er afledt. Her er et spørgsmål, hvilken type bevægelse udført af bungee jumping?