Hvad er Gauss lov: teori og dens betydning

Da videnskabens omfang i vid udstrækning forbedres og indgår i forskellige udviklinger og teknologier, jo mere vi lærer jo mere får vi viden. Og det eneste afgørende emne, som vi skal være opmærksom på, er Gauss-lov, der analyserer elektrisk ladning ud over overfladen og begrebet elektrisk strøm . Loven blev oprindeligt artikuleret af Lagrange i år 1773 og blev derefter understøttet af Friedrich i 1813. Denne lov er en af ​​Maxwell foreslåede fire ligninger, hvor dette er et grundlæggende koncept for klassisk elektrodynamik. Så lad os dykke mere ind i konceptet og kende alle de relaterede begreber i Gauss-loven.

Hvad er Gauss-loven?

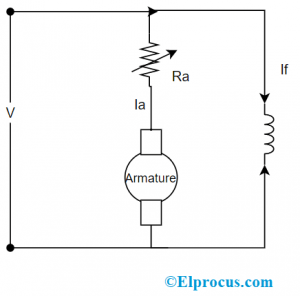
Gauss-loven kan defineres i både begreberne magnetiske og elektriske strømninger. Med hensyn til elektricitet definerer denne lov, at elektrisk strøm gennem hele den lukkede overflade har direkte forhold til den samlede elektriske ladning, der er lukket af overfladen. Det indikerer, at de isolerede elektriske ladninger eksisterer, og sådanne lignende ladninger afvises, mens forskellige ladninger bliver tiltrukket. Og i scenariet med magnetisme siger denne lov, at magnetisk flux gennem den lukkede overflade er nul. Og gauss-loven synes at være stabil i den undersøgelse, som den adskilte magnetiske poler Eksisterer ikke. Det Gauss lovdiagram er vist som nedenfor:

Gauss lovdiagram

Denne lov kan enten defineres som, at den elektriske nettostrøm i den lukkede overflade er lig med den elektriske ladning i overensstemmelse med permittivitet.

F_elektrisk= Q / er₀

Hvor 'Q' svarer til hele den elektriske ladning inden i den lukkede overflade

'er₀'Svarer til den elektriske konstante faktor

Dette er det grundlæggende Gauss lovformel .

Gauss Law Derivation

Gauss-loven betragtes som det relaterede koncept i Coulombs lov, som tillader evaluering af det elektriske felt i flere konfigurationer. Denne lov korrelerer de elektriske feltlinjer, der skaber plads på tværs af overfladen, som omslutter den elektriske ladning 'Q' internt på overfladen. Lad os antage, at Gauss-loven som i retten til Coulombs lov, hvor den er repræsenteret som følger:

E = (1 / (4∏є₀)). (Q / r^to)

Hvor EA = Q / є₀

I ovenstående Gauss lov matematisk udtryk , 'A' svarer til nettoarealet, der omslutter den elektriske ladning, der er 4∏ r^to. Gauss-loven er mere anvendelig og fungerer, når de elektriske ladelinier er justeret i en vinkelret position til overfladen, hvor 'Q' svarer til den elektriske ladning internt til den lukkede overflade.

Når en del af overfladen ikke er justeret i den retvinklede position til den lukkede overflade, vil en faktor cosϴ blive kombineret, som bevæger sig til nul, når de elektriske feltlinjer er i en parallel position til overfladen. Her betyder udtrykket vedlagt, at overfladen skal være fri for enhver form for huller eller huller. Udtrykket 'EA' repræsenterer elektrisk strøm, der kan relateres til de samlede elektriske ledninger, der er adskilt fra overfladen. Ovenstående koncept forklarer gauss lovafledning .

Da Gauss-lovgivning finder anvendelse i mange situationer, er det især fordelagtigt at foretage håndberegninger, når der findes øgede symmetriniveauer i det elektriske felt. Disse forekomster inkluderer cylindrisk symmetri og sfærisk symmetri. Det Gauss lov SI enhed er newtonmeter kvadrat pr. coulomb, hvilket er N m^toC^-1.

Gauss-lovgivning i dielektrikum

For en dielektrisk stof , varierer det elektrostatiske felt på grund af polarisationen, da det også adskiller sig i vakuum. Så Gauss-loven er repræsenteret som

∇E = ρ / є₀

Dette gælder selv i vakuumet og genovervejes for det dielektriske stof. Dette kan skildres i to tilgange, og de er forskellige og integrerede former.

Gauss-loven for magnetostatik

Det grundlæggende koncept for magnetfelter, hvor det varierer fra de elektriske felter, er feltlinjerne, der producerer de omgivede sløjfer. Magneten observeres ikke som halvt for at adskille syd- og nordpolen.

Den anden tilgang er, at det i lyset af magnetfelter synes at være let at observere, at den samlede magnetiske flux, der passerer gennem den lukkede (Gaussiske) overflade, er nul. Den ting, der bevæger sig internt til overfladen, skal ud. Dette angiver Gauss-loven for magnetostatik, hvor den kan repræsenteres som

ʃB.dS = 0 = µʃHds cosϴ = 0

Dette betegnes også som princippet om magnetisk fluxbevaring.

µcosϴʃI = 0, hvilket antyder, at ʃI = 0

Så nettosummen af ​​strømmen, der bevæger sig ind i den lukkede overflade, er nul.

Betydning

Dette afsnit giver en klar forklaring af betydningen af ​​Gauss-loven .

Gauss's lovudtalelse er korrekt for enhver form for lukket overflade uden at være afhængig af størrelsen eller formen på objektet.

Udtrykket 'Q' i den grundlæggende formel for loven består af konsolidering af alle afgifter, de er helt lukket uanset nogen position internt på overfladen.

I tilfældet eksisterer den valgte overflade der både de interne og eksterne ladninger i det elektriske felt (hvor fluxen er til stede i venstre position skyldes de elektriske ladninger i både ind og ud af 'S').

Mens faktor 'q' i den rigtige position af Gauss-loven betyder, at den komplette elektriske ladning internt i 'S'.

Den valgte overflade til funktionaliteten af ​​Gauss-loven kaldes Gaussisk overflade, men denne overflade skal ikke føres gennem nogen form for isolerede ladninger. Dette skyldes årsagen til, at isolerede ladninger ikke nøjagtigt er defineret i den elektriske ladningsposition. Når du kommer tættere på den elektriske ladning, forbedres marken uden nogen grænse. Mens den Gaussiske overflade gennemgår den kontinuerlige ladetildeling.

Gauss-loven anvendes hovedsageligt til en mere forenklet analyse af det elektrostatiske felt i scenariet, hvor systemet har en vis ligevægt. Dette accelereres kun ved valg af en passende Gaussisk overflade.

I det store og hele er denne lov afhængig af den omvendte firkant baseret på placeringen i Coulombs lov. Enhver form for brud på Gauss-loven vil betyde afvigelsen fra den omvendte lov.

Eksempler

Lad os overveje nogle få gauss lov eksempler :

1). En lukket gaussisk overflade i 3D-rummet, hvor den elektriske flux måles. Forudsat at den gaussiske overflade er kugleformet, er den lukket med 30 elektroner og har en radius på 0,5 meter.

• Beregn den elektriske strøm, der passerer gennem overfladen
• Find den elektriske flux, der har en afstand på 0,6 meter til feltet målt fra overfladens centrum.
• Kend forholdet, der findes mellem den lukkede ladning og den elektriske flux.

Svar a.

Med formlen for elektrisk strøm kan nettoladningen, der er lukket i overfladen, beregnes. Dette kan opnås ved opladningsmultiplikation for elektronen med hele elektronerne, der vises på overfladen. Ved hjælp af dette kan man kende den frie pladsgennemtrængelighed og den elektriske strømning.

= = Q / er₀= [30 (1,60 * 10-¹⁹) /8,85 * 10^-12]

= 5,42 * 10^-12Newton * meter / Coulomb

Svar b.

Omarrangering af ligningen af ​​elektrisk strøm og ekspression af arealet pr. Radius kan bruges til at beregne det elektriske felt.

Ф = EA = 5,42 * 10^-12Newton * meter / Coulomb

E = (5,42 * 10^-)/TIL

= (5,42 * 10^-) / 4∏ (0,6)^to

Da den elektriske strømning har en direkte andel med den medfølgende elektriske ladning, betyder det, at når den elektriske ladning på overfladen forbedres, vil også strømmen, der passerer gennem den, blive forbedret.

2). Overvej en kugle med en radius på 0,12 meter, der har en lignende ladningsfordeling på overfladen. Denne kugle har et elektrisk felt placeret i en afstand på 0,20 meter, som har en værdi på -10 Newton / Coulomb. Beregn

• Beregn mængden af ​​elektrisk ladning, der spredes på kuglen?
• Definer hvorfor eller hvorfor ikke det elektriske felt, der er internt i sfæren, er nul?

Svar a.

For at kende Q er formlen, vi bruger her

E = Q / (4∏r^toer₀ER)

Med dette Q = 4∏ (0,20)^to(8,85 * 10^-12) (- 100)

Q = 4,45 * 10^-10C

Svar b.

I det tomme sfæriske rum findes der ingen elektrisk ladning internt med total ladning, der lever på overfladen. Da der ikke er nogen intern opladning, er det elektriske felt, der er internt i sfæren, også nul.

Anvendelser af Gauss-loven

Få af de applikationer, hvor denne lov anvendes, er som forklaret nedenfor:

• Det elektriske felt mellem de to parallelt placerede kondensatorplader er E = σ / є0, hvor 'σ' svarer til densiteten af ​​overfladeladningen.
• Det elektrisk feltintensitet som er placeret nær det plane ark med ladning er E = σ / 2є₀K og σ svarer til densiteten af ​​overfladeladningen
• Den elektriske feltintensitet, der er placeret nær lederen, er E = σ / є₀K og σ svarer til tætheden af ​​overfladeladningen, når mediet vælges som dielektrisk derefter E._luft= σ / er₀
• I scenariet med en uendelig elektrisk ladning placeret i en afstand af radius 'r', så er E = ƴ / 2∏rє₀

For at vælge den Gaussiske overflade skal vi overveje de tilstande, hvor andelen af ​​dielektrisk konstant og den elektriske ladning tilvejebringes af en 2d overflade, der er integreret end ladningsfordelingens elektriske feltsymmetri. Her kommer de tre forskellige situationer:

• I tilfælde, hvor afgiftsallokeringen er i form af cylindrisk symmetrisk
• I tilfælde, hvor afgiftsallokeringen er i form af sfærisk symmetrisk
• Det andet scenario er, at afgiftsallokeringen har translationel symmetri gennem hele planet

Den gaussiske overfladestørrelse vælges ud fra betingelsen om, hvorvidt vi har brug for at måle feltet. Denne sætning er mere nyttig til at kende feltet, når der findes tilsvarende symmetri, fordi den adresserer retning af feltet.

Og dette handler om begrebet Gauss Law. Her har vi gennemgået en detaljeret analyse af at vide, hvad Gauss-loven er, dens eksempler, betydning, teori, formel og anvendelser. Derudover anbefales en mere at kende til fordelene ved Gauss-loven og ulemper ved gauss lov , dets diagram og andre.