Elektroner og huller spiller en vigtig rolle i overførslen af elektricitet i halvledere . Disse partikler er arrangeret på et andet energiniveau i en halvleder. Elektroners bevægelse fra et energiniveau til et andet genererer elektricitet . En elektron inde i metallet skal have et energiniveau, der mindst er større end overfladebarrierenergien for at flygte til et højere energiniveau.
Der var mange afhandlinger foreslået og accepteret, der forklarede elektronernes egenskaber og opførsel. Men en vis opførsel af elektron, såsom uafhængigheden af emissionsstrømmen på temperatur osv. ... forblev stadig et mysterium. Så et gennembrud statistik, Fermi Dirac Statistik , udgivet af Enrico Fermi og Paul Dirac i 1926 hjalp med at løse disse gåder.
Fra da Fermi Dirac-distribution anvendes til at forklare en stjernes sammenbrud til en hvid dværg, til at forklare fri elektronemission fra metaller osv ...
Fermi Dirac-distribution
Før du går ind i Fermi Dirac Distribution-funktion lad os se på energien distribution af elektroner i forskellige typer halvledere. Den maksimale energi af et frit elektron kan have i et materiale ved absolut temperatur, dvs. ved 0k er kendt som Fermi energiniveau. Værdien af Fermi-energi varierer for forskellige materialer. Baseret på den energi, som elektroner har i en halvleder, er elektroner arrangeret i tre energibånd - Ledningsbånd, Fermi energiniveau, Valency-bånd.
Mens ledningsbånd indeholder ophidsede elektroner, indeholder valensbånd huller. Men hvad betød Fermi-niveauet for? Fermi-niveau er energitilstanden, som sandsynligvis ½ bliver optaget af en elektron. Enkelt sagt er det det maksimale energiniveau, som en elektron kan have ved 0k, og sandsynligheden for at finde elektronen over dette niveau ved absolut temperatur er 0. Ved absolut nul temperatur vil halvdelen af Fermi-niveauet blive fyldt med elektroner.
I energibånddiagram over halvleder ligger Fermi-niveau midt i lednings- og valensbånd for en iboende halvleder. For ydre halvleder ligger Fermi-niveau nær valensbånd i P-type halvleder og for N-type halvleder , det ligger tæt på ledningsbåndet.
Fermi energiniveau er betegnet med ERF, ledningsbåndet betegnes som ERC og valensbånd betegnes som EV.

Fermi niveau i N og P typer
Fermi-niveau i N- og P-halvledere
Fermi Dirac-distributionsfunktion
Sandsynligheden for, at den tilgængelige energitilstand 'E' vil blive optaget af en elektron ved absolut temperatur T under betingelser med termisk ligevægt, gives af Fermi-Dirac-funktionen. Fra kvantefysik er Fermi-Dirac Distribution Expression
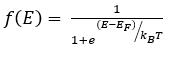
Hvor k er Boltzmann konstant i ELLERTIL , T er temperaturen i 0TIL og ERF er Fermi-energiniveauet i eV.k = 1,38X10-2. 3J / K
Fermi-niveauet repræsenterer energitilstanden med en 50% sandsynlighed for at blive fyldt, hvis der ikke findes noget forbudt bånd, dvs. E = EF derefter f (E) = 1/2 for enhver temperaturværdi.
Fermi-Dirac-distribution giver kun sandsynligheden for statens belægning på et givet energiniveau, men giver ingen oplysninger om antallet af tilgængelige stater på dette energiniveau.
Fermi Dirac Distribution and Energy Band Diagram

f (E) Vs (E-EF) grund
Ovenstående plot viser Fermi-niveauets opførsel ved forskellige temperaturområder T = 00K, T = 3000K, T = 25000TIL. På T = 0K , kurven har trinlignende egenskaber.
På T = 00TIL , kan det samlede antal energiniveauer optaget af elektroner kendes ved hjælp af Fermi-Dirac-funktionen.
For et givet energiniveau E> EF bliver det eksponentielle udtryk i Fermi-Dirac-funktionen 0 og hvilket betyder, at sandsynligheden for at finde det besatte energiniveau af energi større end ERF er nul.
For et givet energiniveau ER
Til temperaturer, der er højere end absolut temperatur og E = EF derefter uafhængig af temperaturens værdi.
Til temperaturer, der er højere end absolut temperatur og ER
Til temperaturer, der er højere end absolut temperatur og E> EF , vil den eksponentielle være positiv og øges med E. f (E) starter fra 0,5 og har tendens til at falde mod 0, når E øges.
Fermi Dirac Distribution Boltzmann tilnærmelse
Maxwell-Boltzmann-distribution er den mest anvendte Fermi Dirac fordeling tilnærmelse .
Fermi-Dirac Distribution gives af 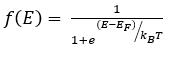
Ved ved hjælp af Maxwell - Boltzmann-tilnærmelse ovenstående ligning er reduceret til

Når forskellen mellem transportørens energi og Fermi-niveau er stor sammenlignet med, kan udtrykket 1 i nævneren ignoreres. Til anvendelse af Fermi-Dirac-distribution skal elektronen følge Paulis eksklusive princip, hvilket er vigtigt ved høj doping. Men distributionen af Maxwell-Boltzmann forsømmer dette princip, og Maxwell-Boltzmann-tilnærmelsen er derfor begrænset til dårligt dopede tilfælde.
Fermi Dirac og Bose-Einstein Statistik
Fermi-Dirac-statistik er en gren af kvantestatistikker, der beskriver fordelingen af partikler i energitilstande, der indeholder identiske partikler, der adlyder Pauli-eksklusionsprincippet. Da F-D-statistikker anvendes på partikler med halvtalt spin, kaldes disse fermioner.
Et system bestående af termodynamisk ved ligevægt og identiske partikler, i enkeltpartikel-tilstand I, er det gennemsnitlige antal fermioner givet ved F-D-fordeling som 
hvor er tilstanden med en enkelt partikel jeg , er det samlede kemiske potentiale betegnet med, tilB er Boltzmann konstant, mens T er den absolutte temperatur.
Bose-Einstein statistik er det modsatte af F-D statistik. Dette anvendes på partikler med fuldt hel spin eller intet spin, kaldet Bosons. Disse partikler adlyder ikke Pauli-eksklusionsprincippet, hvilket betyder, at den samme kvantekonfiguration kan udfyldes med mere end en boson.
F-D-statistik og Bore-Einstein-statistik anvendes, når kvanteeffekten er vigtig, og partiklerne ikke kan skelnes.
Fermi Dirac Distribution Problem
Overvej i et solidt energiniveau, der ligger 0,11 eV under Fermi-niveauet. Find sandsynligheden for, at dette niveau ikke optages af elektronen?

Fermi Dirac Distribution Problem
Dette handler om Fermi Dirac-distribution . Fra ovenstående information kan vi endelig konkludere, at et systems makroskopiske egenskaber kan beregnes ved hjælp af en Fermi-Dirac-funktion. Det bruges til at kende Fermi energi i både nul og endelige temperatur tilfælde. Lad os besvare et spørgsmål uden beregninger baseret på vores forståelse af Fermi-Dirac distribution. For et energiniveau E, 0,25e.V under Fermi-niveauet og temperaturen over den absolutte temperatur, falder Fermi-distributionskurven mod 0 eller stiger mod 1?