De forskellige former for kanonisk udtryk, der inkluderer summen af produkter (SOP) og produkter af summen (POS), kanonisk udtryk kan defineres som en Boolsk udtryk som enten har min sigt ellers max sigt. For eksempel, hvis vi har to variabler, nemlig X & Y, vil det kanoniske udtryk, der omfatter min termer, være XY + X'Y ', hvorimod det kanoniske udtryk, der omfatter maksimale udtryk, er (X + Y) (X' + Y ' ). Denne artikel diskuterer en oversigt over summen af produkter og produkter fra Sums, typer af SOP og POS, skematisk design og K-map.
Summen af produkter og produkt af sum
Begrebet sum af produkter (SOP) Omfatter primært minterm, typer af SOP, K-map og skematisk design af SOP. På samme måde inkluderer produktet af beløb (POS) hovedsagelig maks. term , typer af produkt af beløb , k-map og skematisk design af POS.
Hvad er en sum af produktet (SOP)?
Den korte form for summen af produktet er SOP, og det er en slags Boolsk algebra udtryk. I dette tilføjes de forskellige produktindgange sammen. Produktet af input er boolsk logisk OG mens summen eller tilføjelsen er boolsk logisk ELLER. Før vi forstår begrebet summen af produkter, skal vi kende begrebet minterm.
Det min periode kan defineres som, når minimumskombinationerne af input er høje, vil output være højt. Det bedste eksempel på dette er AND gate, så vi kan sige, at min term er kombinationer af AND gate input. Sandhedstabellen for min. Periode er vist nedenfor.
x | Y | MED | Min sigt (m) |
0 | 0 | 0 | X'Y'Z '= m0 |
0 | 0 | 1 | X’Y’Z = m1 |
0 | 1 | 0 | X'Y Z '= m2 |
| 0 | 1 | 1 | X’YZ = m3 |
| 1 | 0 | 0 | XY'Z '= m4 |
1 | 0 | 1 | XY'Z = m5 |
| 1 | 1 | 0 | XYZ ’= m6 |
| 1 | 1 | 1 | XYZ = m7 |
I ovenstående tabel er der tre indgange, nemlig X, Y, Z, og kombinationerne af disse indgange er 8. Hver kombination har en minterm, der er specificeret med m.
Typer af produktsummen (SOP)
Det summen af produkter er tilgængelig i tre forskellige former som inkluderer følgende.
- Kanonisk sum af produkter
- Ikke-kanonisk sum af produkter
- Minimal sum af produkter
1). Kanonisk sum af produkter
Dette er en normal form for SOP, og den kan dannes ved at gruppere mintermerne for den funktion, for hvilken o / p er høj eller sand, og det kaldes også som summen af mintermer. Udtrykket af den kanoniske SOP betegnes med tegnsammensætning (∑), og mintermerne i parentes tages, når output er sandt. Sandhedstabellen for den kanoniske sum af produktet er vist nedenfor.
x | Y | MED | F |
0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
For ovenstående tabel er kanonisk SOP-form kan skrives som F = ∑ (m1, m2, m3, m5)
Ved at udvide ovenstående summering kan vi få følgende funktion.
F = m1 + m2 + m3 + m5
Ved at erstatte mintermerne i ovenstående ligning kan vi få nedenstående udtryk
F = X'Y'Z + X'YZ '+ X'YZ + XY'Z
Produktbetegnelsen for den kanoniske form inkluderer både komplementerede og ikke-komplimenterede input
2). Ikke-kanonisk sum af produkter
I den ikke-kanoniske sum af produktform er produktbetingelserne forenklet. Lad os f.eks. Tage det ovennævnte kanoniske udtryk.
F = X'Y'Z + X'YZ '+ X'YZ + XY'Z
F = X'Y'Z + X'Y (Z '+ Z) + XY'Z
Her Z ’+ Z = 1 (Standardfunktion)
F = X'Y'Z + X'Y (1) + XY'Z
F = X'Y'Z + X'Y + XY'Z
Dette er stadig i form af SOP, men det er den ikke-kanoniske form
3). Minimal sum af produkter
Dette er det mest forenklede udtryk for produktets sum, og det er også en type ikke-kanonisk. Denne type dåse er forenklet med den boolske algebraiske sætninger selvom det simpelthen gøres ved hjælp af K-kort (Karnaugh-kort) .
Denne formular vælges på grund af antallet af inputlinjer & porte bruges i dette er minimum. Det er rentabelt nyttigt på grund af sin solide størrelse, hurtige hastighed sammen med den lave fremstillingspris.
Lad os tage et eksempel på den kanoniske formfunktion og den minimale Kort over produkter K er

SOP K-kort
Udtrykket af dette baseret på K-kortet vil være
F = Y'Z + X'Y
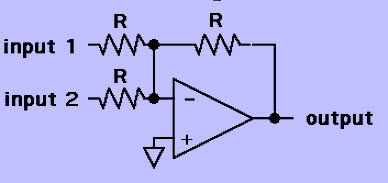
Skematisk design af summen af produktet
Udtrykket af produktsummen udfører AND-ELLER-design i to niveauer, og dette design kræver en samling af AND-porte og en ELLER-port. Hvert udtryk for produktsummen har samme design.

Skematisk design af SOP
Antallet af input og antallet af AND-porte afhænger af det udtryk man implementerer. Designet for en minimal sum af produkt og kanonisk udtryk ved hjælp af AND-ELLER-porte er vist ovenfor.
Hvad er et produkt af sum (POS)?
Den korte form for summen af produktet er POS, og det er en slags boolsk algebraudtryk. I dette er det en form, hvor der tages produkter af den forskellige sum af input, som ikke er aritmetiske resultat & sum, selvom de er logiske boolske OG & ELLER tilsvarende. Inden vi går i gang med at forstå konceptet med produktet af summen, skal vi kende begrebet maks. Udtryk.
Maxterm kan defineres som et udtryk, der er sandt for det højeste antal inputkombinationer, ellers er det falskt for single inputkombinationer. Fordi OR gate også giver falsk for kun en inputkombination. Således er Max-udtrykket ELLER af ethvert suppleret ellers ikke-komplementeret input.
x | Y | MED | Max sigt (M) |
0 | 0 | 0 | X + Y + Z = M0 |
| 0 | 0 | 1 | X + Y + Z '= M1 |
0 | 1 | 0 | X + Y ’+ Z = M2 |
| 0 | 1 | 1 | X + Y ’+ Z’ = M3 |
1 | 0 | 0 | X ’+ Y + Z = M4 |
| 1 | 0 | 1 | X '+ Y + Z' = M5 |
1 | 1 | 0 | X '+ Y' + Z = M6 |
| 1 | 1 | 1 | X ’+ Y’ + Z ’= M7 |
I ovenstående tabel er der tre indgange, nemlig X, Y, Z, og kombinationerne af disse indgange er 8. Hver kombination har en maksimal term, der er specificeret med M.
I maksimumsperiode suppleres hvert input, da det kun giver '0', mens den angivne kombination anvendes og komplement af minterm er et maksimalt udtryk.
M3 = m3 '
(X'YZ) '= M3
X + Y ’+ Z’ = M3 (De Morgan's Law)
Typer af produkt af sum (POS)
Produktet af summen er klassificeret i tre typer, der inkluderer følgende.
- Canonical Product of Sums
- Ikke-kanonisk produkt af sums
- Minimalt produkt af summer
1). Kanonisk produkt af sum
Den kanoniske POS er også navngivet som et produkt med maks. Term. Disse er OG sammen, for hvilke o / p er lav eller falsk. Udtrykket dette betegnes med ∏, og de maksimale udtryk i parentes tages, når output er falsk. Sandhedstabellen for det kanoniske produkt af sum er vist nedenfor.
x | Y | MED | F |
| 0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
For ovenstående tabel kan den kanoniske POS skrives som F = ∏ (M0, M4, M6, M7)
Ved at udvide ovenstående ligning kan vi få følgende funktion.
F = M0, M4, M6, M7
Ved at erstatte de maksimale termer i ovenstående ligning kan vi få nedenstående udtryk
F = (X + Y + Z) (X '+ Y + Z) (X' + Y '+ Z) (X' + Y '+ Z')
Produktbetegnelsen for den kanoniske form inkluderer både komplementerede og ikke-komplimenterede input
2). Ikke - kanonisk produkt af sum
Udtrykket af produkt af sum (POS) ikke er i normal form navngives som ikke-kanonisk form. Lad os f.eks. Tage ovenstående udtryk
F = (X + Y + Z) (X '+ Y + Z) (X' + Y '+ Z) (X' + Y '+ Z')
F = (Y + Z) (X '+ Y + Z) (X' + Y '+ Z')
Lignende, selvom omvendte udtryk fjernes fra to maksimale udtryk og former, er kun udtryk for at vise det her er en forekomst.
= (X + Y + Z) (X '+ Y + Z)
= XX ’+ XY + XZ + X’Y + YY + YZ + X’Z + YZ + ZZ
= 0 + XY + XZ + X’Y + YY + YZ + X’Z + YZ + Z
= X (Y + Z) + X '(Y + Z) + Y (1 + Z) + Z
= (Y + Z) (X + X ') + Y (1) + Z
= (Y + Z) (0) + Y + Z
= Y + Z
Ovenstående endelige udtryk er stadig i form af produkt af sum, men det er i form af ikke-kanonisk.
3). Minimalt produkt af summer
Dette er det mest forenklede udtryk for summen af produktet, og det er også en type ikke-kanonisk. Denne type dåse er gjort forenklet med de boolske algebraiske sætninger, selvom det simpelthen gøres ved hjælp af K-map (Karnaugh-kort).
Denne formular vælges på grund af antallet af inputlinjer og porte, der bruges i dette er minimum. Det er rentabelt nyttigt på grund af sin solide størrelse, hurtige hastighed sammen med den lave fremstillingspris.
Lad os tage et eksempel på kanonisk formfunktion, og Produkt af summer K-kort er

POS K-kort
Udtrykket af dette baseret på K-kortet vil være
F = (Y + Z) (X ’+ Y’)
Skematisk design af produkt af sum
Ekspressionen af produktet af summen udfører to niveauer OR- AND-design, og dette design kræver en samling af OR-porte og en AND-port. Hvert udtryk for sumproduktet har samme design.

Skematisk design af POS
Antallet af input og antallet af AND-porte afhænger af det udtryk man implementerer. Designet til en minimal sum af produkt og kanonisk udtryk ved hjælp af OR-AND-porte er vist ovenfor.
Således handler det hele om Kanoniske formularer : Summen af produkter og Sums-produkter, skematisk design, K-map osv. Fra ovenstående information kan vi endelig konkludere, at et boolsk udtryk består fuldstændigt af minterm, ellers navngives maxterm som det kanoniske udtryk. Her er et spørgsmål til dig, hvad er de to former for kanoniske udtryk?