Sådan beregnes modificeret sinusbølgeform

Jeg er sikker på, at du måske ofte har spekuleret på, hvordan man opnår den korrekte måde at optimere og beregne en modificeret firkantbølge på, således at den producerede næsten en identisk replikering af en sinusbølge, når den bruges i en inverterapplikation.

Beregningerne diskuteret i denne artikel hjælper dig med at lære den teknik, hvorigennem et modificeret firkantbølgekredsløb kunne omdannes til sinusbølgeækvivalent. Lad os lære procedurerne.

Det første kriterium for at opnå dette er at matche RMS-værdien af ​​den modificerede firkant med sinusbølgemodellen på en måde, så resultatet replikerer den sinusformede bølgeform så tæt som muligt.

Hvad er RMS (Root Mean Square)

Vi ved, at RMS for vores hjem AC sinusformede bølgeformspænding bestemmes ved at løse følgende forhold:

V spids = √2 V. rms

Hvor V spids er den maksimale eller maksimumsgrænsen for sinusbølgeformcyklussen, mens gennemsnitsstørrelsen af ​​hver cyklus af bølgeformen er vist som V rms

Det √2 i formlen hjælper os med at finde middelværdi eller nettoværdien af ​​en vekselstrømscyklus, der ændrer spændingen eksponentielt med tiden. Da den sinusformede spændingsværdi varierer med tiden og er en funktion af tiden, kan den ikke beregnes ved at anvende den grundlæggende gennemsnitlige formel, i stedet afhænger vi af ovenstående formel.

Alternativt kunne AC RMS forstås som en ækvivalent med den værdi af en jævnstrøm (DC), der producerer en identisk gennemsnitlig effekttab, når den er forbundet over en resistiv belastning.

OK, så nu kender vi formlen til beregning af RMS for en sinusbølgecyklus med reference til dens spidsværdi.

Dette kan også anvendes til evaluering af toppen og RMS til vores hjem 50 Hz AC. Ved at løse dette får vi RMS som 220V og topper som 310V for alle 220V baserede netstrømssystemer.

Beregning af modificeret firkantbølge RMS og Peak

Lad os nu se, hvordan dette forhold kan anvendes i modificerede firkantbølgeomformere til opsætning af de rigtige bølgeformscyklusser til et 220V-system, hvilket svarer til en 220V AC sinusformet ækvivalent.

Vi ved allerede, at AC RMS svarer til gennemsnitseffekten af ​​en DC-bølgeform. Hvilket giver os dette enkle udtryk:

V spids = V rms

Men vi ønsker også, at firkantbølgens top skal være på 310V, så det ser ud til, at ovenstående ligning ikke holder godt og ikke kan bruges til formålet.

Kriterierne er at have 310V peak såvel som en RMS eller gennemsnitlig værdi på 220V for hver firkantbølgecyklus.

For at løse dette korrekt tager vi hjælp af ON / OFF-tiden for de firkantede bølger eller driftscyklusprocenten som forklaret nedenfor:

Hver halve cyklus af en 50 Hz AC-bølgeform har en tidsvarighed på 10 millisekunder (ms).

En modificeret halvbølgecyklus i sin mest rå form skal se ud som vist i følgende billede:

Vi kan se, at hver cyklus begynder med et nul- eller tomrum, derefter skyder op til 310V peak-puls og slutter igen med et 0V-mellemrum, processen gentages derefter for anden halvcyklus.

For at opnå den krævede 220V RMS er vi nødt til at beregne og optimere top- og nulafstandssektionerne eller ON / OFF-perioderne i cyklussen, så gennemsnitsværdien producerer den krævede 220V.

Den grå linje repræsenterer cyklusens 50% periode, som er 10 ms.

Nu skal vi finde ud af proportionerne af ON / OFF-tiden, som producerer et gennemsnit på 220V. Vi gør det på denne måde:

220/310 x 100 = ca. 71%

Dette viser, at 310V-spidsen i den ovenfor modificerede cyklus skal indtage 71% af 10 ms-perioden, mens de to nul-huller skal være 29% kombineret eller 14,5% hver.

Derfor, i en længde på 10 ms, skal det første nul-afsnit være 1,4 ms, efterfulgt af 310 V-spidsen i 7 ms, og endelig det sidste nul-hul på yderligere 1,4 ms.

Når dette er opnået, kan vi forvente, at output fra inverteren producerer en rimelig god replikation af en sinusbølgeform.

På trods af alle disse kan du opleve, at output ikke er en ideel replikering af sinusbølgen, fordi den diskuterede modificerede firkantbølge er i sin mest basale form eller en rå type. Hvis vi ønsker, at output skal matche sinusbølgen med maksimal præcision, så er vi nødt til at gå efter en SPWM tilgang .

Jeg håber, at ovenstående diskussion måske har oplyst dig om, hvordan du beregner og optimerer en modificeret firkant til replikering af sinusbølgeoutput.

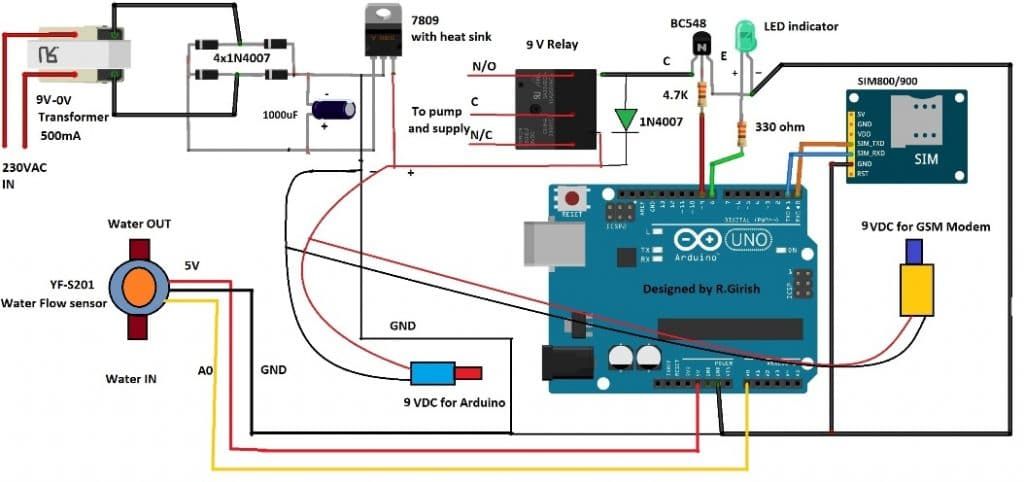
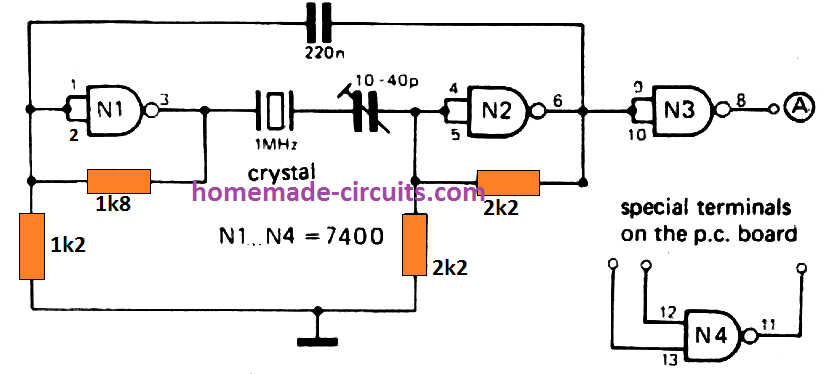
For praktisk verifikation kan læserne prøve at anvende ovennævnte teknik til dette simpelt modificeret inverter kredsløb.

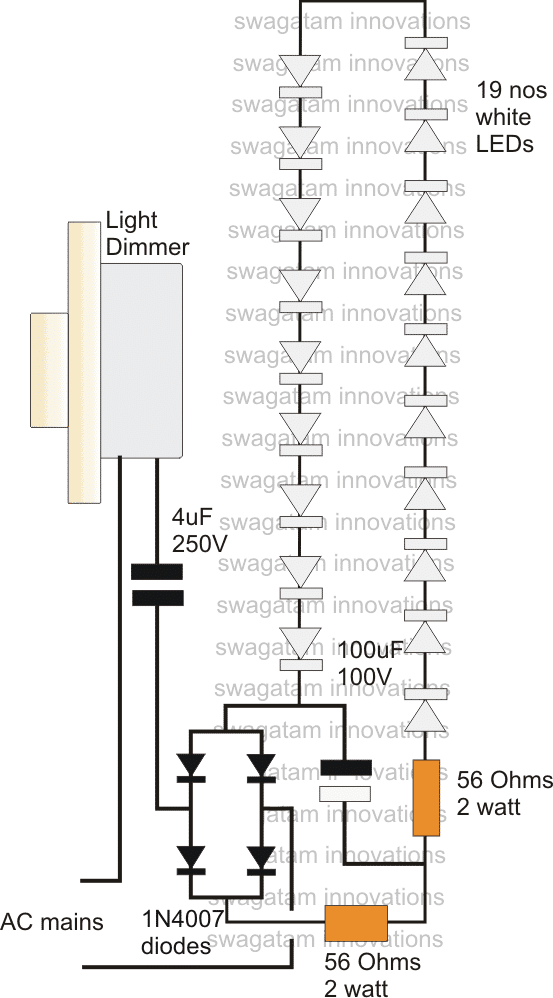
Her er en anden klassisk eksempel på en optimeret modificeret bølgeform for at få en god sinusbølge ved transformatorens sekundær.