Beregning af ferritransformator er en proces, hvor ingeniører vurderer de forskellige viklingsspecifikationer og kernedimensionen af transformeren ved hjælp af ferrit som kernematerialet. Dette hjælper dem med at oprette en perfekt optimeret transformer til en given applikation.
Indlægget præsenterer en detaljeret forklaring på, hvordan man beregner og designer tilpassede ferritkernetransformere. Indholdet er let at forstå og kan være meget praktisk for ingeniører, der beskæftiger sig med kraftelektronik og fremstilling af SMPS-omformere.

Hvorfor ferritkerne bruges i højfrekvensomformere
Du har måske ofte undret dig over årsagen til brugen af ferritkerner i alle moderne switch mode strømforsyninger eller SMPS konvertere. Ret, det er at opnå højere effektivitet og kompakthed sammenlignet med jernkerne strømforsyninger, men det ville være interessant at vide, hvordan ferritkerner tillader os at opnå denne høje grad af effektivitet og kompakthed?
Det er fordi i jernkernetransformere, jernmaterialet har meget ringere magnetisk permeabilitet end ferritmateriale. I modsætning hertil har ferritkerner meget høj magnetisk permeabilitet.
Betydning, når ferritmateriale udsættes for et magnetfelt, er det i stand til at opnå en meget høj grad af magnetisering bedre end alle andre former for magnetisk materiale.
En højere magnetisk permeabilitet betyder lavere mængde hvirvelstrøm og lavere skiftetab. Et magnetisk materiale har normalt en tendens til at generere hvirvelstrøm som reaktion på en stigende magnetisk frekvens.
Efterhånden som frekvensen øges, øges virvelstrømmen også, hvilket forårsager opvarmning af materialet og øges i spoleimpedans, hvilket fører til yderligere koblingstab.
Ferritkerner er på grund af deres høje magnetiske permeabilitet i stand til at arbejde mere effektivt med højere frekvenser på grund af lavere hvirvelstrømme og lavere skiftetab.
Nu kan du tænke, hvorfor ikke bruge lavere frekvens, da det omvendt ville hjælpe med at reducere hvirvelstrømme? Det ser ud til at være gyldigt, men lavere frekvens vil også betyde at øge antallet af drejninger for den samme transformer.
Da højere frekvenser tillader forholdsmæssigt lavere antal drejninger, resulterer transformatoren i at være mindre, lettere og billigere. Dette er grunden til, at SMPS bruger en høj frekvens.
Inverter Topologi
I omskifter i omskiftertilstand udgår normalt to typer topologi: push-pull og Fuld bro . Skubtrækket anvender et centerhane til den primære vikling, mens den fulde bro består af en enkelt vikling til både primær og sekundær.
Faktisk er begge topologien push-pull i naturen. I begge former påføres viklingen med en kontinuerligt skiftende tilbagegående vekselstrøm af MOSFET'erne, der oscillerer ved den specificerede høje frekvens og efterligner en push-pull-handling.
Den eneste grundlæggende forskel mellem de to er, at den primære side af centerhanetransformatoren har 2 gange mere antal drejninger end Full bridge-transformeren.
Sådan beregnes ferritkerneomformertransformer
Beregning af en ferritkernetransformator er faktisk ret enkel, hvis du har alle de angivne parametre i hånden.
For enkelheds skyld forsøger vi at løse formlen gennem et eksempel, der er oprettet, lad os sige for en 250 watt transformer.
Strømkilden vil være et 12 V batteri. Frekvensen for at skifte transformator vil være 50 kHz, en typisk figur i de fleste SMPS-invertere. Vi antager, at output er 310 V, hvilket normalt er topværdien af en 220V RMS.
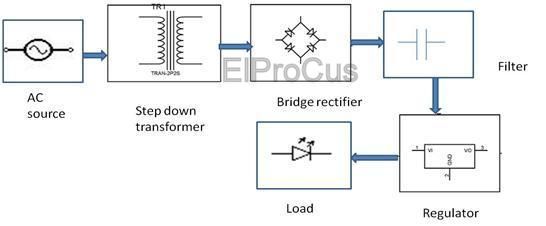
Her vil 310 V være efter afhjælpning gennem hurtig genopretning bro ensretter og LC-filtre. Vi vælger kernen som ETD39.
Som vi alle ved, når en 12 V batteri bruges, er spændingen aldrig konstant. Ved fuld opladning er værdien omkring 13 V, hvilket fortsætter med at falde, når inverterbelastningen bruger strøm, indtil batteriet endelig aflades til den laveste grænse, som typisk er 10,5 V. Så for vores beregninger vil vi betragte 10,5 V som forsyningsværdien for V om (min).
Primære vendinger
Standardformlen til beregning af det primære antal drejninger er angivet nedenfor:
N (først)= V i (substantiv)x 108/ 4 x f x B maksx TIL c
Her N (først)henviser til de primære svingnumre. Da vi i vores eksempel har valgt en center-tryk-træk-topologi, vil det opnåede resultat være halvdelen af det samlede antal drejninger, der kræves.
- Vin (efternavn)= Gennemsnitlig indgangsspænding. Da vores gennemsnitlige batterispænding er 12V, lad os tage Vin (efternavn)= 12.
- f = 50 kHz eller 50.000 Hz. Det er den foretrukne skiftefrekvens, som valgt af os.
- B maks= Maksimal fluxdensitet i Gauss. I dette eksempel antager vi B maksat være i området fra 1300G til 2000G. Dette er standardværdien for de fleste ferritbaserede transformerkerner. Lad os i dette eksempel afregne ved 1500G. Så det har vi gjort B maks= 1500. Højere værdier på B maksanbefales ikke, da dette kan resultere i, at transformeren når mætningspunktet. Omvendt lavere værdier af B makskan resultere i, at kernen bliver underudnyttet.
- TILc= Effektivt tværsnitsareal i cmto. Disse oplysninger kan indsamles fra databladene for ferritkernerne . Du kan også finde Acbliver præsenteret som Aer. For det valgte kernenummer ETD39 er det effektive tværsnitsareal, der er angivet i databladet, 125 mmto. Det svarer til 1,25 cmto. Derfor har vi, Ac= 1,25 for ETD39.
Ovenstående figurer giver os værdierne for alle de parametre, der kræves til beregning af de primære drejninger på vores SMPS-invertertransformator. Derfor erstatter vi de respektive værdier i ovenstående formel:
N (først)= V i (substantiv)x 108/ 4 x f x B maksx TIL c
N (først)= 12 x 108/ 4 x 50000 x 1500 x 1,2
N (først)= 3,2
Da 3.2 er en brøkværdi og kan være vanskelig at implementere praktisk, afrunder vi den til 3 omdrejninger. Før vi afslutter denne værdi, skal vi dog undersøge, om værdien af B makser stadig kompatibel og inden for det acceptable interval for denne nye afrundede værdi 3.
Fordi at mindske antallet af drejninger vil medføre en forholdsmæssig stigning i B maksderfor bliver det bydende nødvendigt at kontrollere, om den øgede B makser stadig inden for acceptabelt interval for vores 3 primære drejninger.
Kontrakontrol B maksved at erstatte følgende eksisterende værdier, vi får:
Vin (efternavn)= 12, f = 50000, N på= 3, TIL c= 1,25
B maks= V i (substantiv)x 108/ 4 x f x N (først)x TIL c
B maks= 12 x 108/ 4 x 50000 x 3 x 1,25
B maks= 1600
Som det kan ses det nye B maksværdi for N (på)= 3 omdrejninger ser fint ud og ligger godt inden for det acceptabelt interval. Dette indebærer også, at hvis du når som helst har lyst til at manipulere antallet af N (først)drejer, skal du sørge for, at den overholder den tilsvarende nye B maksværdi.
Omvendt kan det være muligt først at bestemme B maksfor et ønsket antal primære drejninger, og juster derefter antallet af drejninger til denne værdi ved passende at ændre de andre variabler i formlen.
Sekundære drejninger
Nu ved vi, hvordan man beregner den primære side af en ferrit SMPS-invertertransformator, det er tid til at se på den anden side, det er sekundæren til transformeren.
Da topværdien skal være 310 V for sekundæren, vil vi ønske, at værdien opretholdes for hele batterispændingsområdet fra 13 V til 10,5 V.
Vi er uden tvivl nødt til at ansætte en feedback system til at opretholde et konstant udgangsspændingsniveau, til at modvirke lav batterispænding eller stigende variationer i belastningsstrømmen.
Men til dette skal der være en øvre margen eller et headroom for at lette denne automatiske kontrol. En +20 V margen ser godt nok ud, derfor vælger vi den maksimale udgangsspænding som 310 + 20 = 330 V.
Dette betyder også, at transformeren skal være designet til at afgive 310 V ved den laveste 10,5 batterispænding.
Til feedbackkontrol anvender vi normalt et selvjusterende PWM-kredsløb, der udvider pulsbredden under lavt batteri eller høj belastning og indsnævrer det forholdsmæssigt uden belastning eller optimale batteriforhold.
Dette betyder, ved lave batteri forhold PWM skal automatisk justeres til maksimal driftscyklus for at opretholde den foreskrevne 310 V output. Denne maksimale PWM kan antages at være 98% af den samlede driftscyklus.
2% -gabet er tilbage til dødtiden. Død tid er nul spændingsgabet mellem hver halve cyklusfrekvens, hvor MOSFET'erne eller de specifikke strømforsyningsenheder forbliver helt lukket. Dette sikrer garanteret sikkerhed og forhindrer skydning gennem MOSFET'erne i overgangsperioderne for push pull-cyklusser.
Derfor vil indgangsforsyningen være minimal, når batterispændingen når på sit minimumsniveau, det er når V i= V om (min)= 10,5 V. Dette vil medføre, at driftscyklussen maksimalt er 98%.
Ovenstående data kan bruges til beregning af den gennemsnitlige spænding (DC RMS), der kræves til transformatorens primære side for at generere 310 V ved sekundær, når batteriet er på mindst 10,5 V. For dette multiplicerer vi 98% med 10,5, som vist nedenfor:
0,98 x 10,5 V = 10,29 V, dette er den spændingsvurdering, som vores transformator primære skal have.
Nu kender vi den maksimale sekundære spænding, der er 330 V, og vi kender også den primære spænding, der er 10,29 V. Dette giver os mulighed for at få forholdet mellem de to sider som: 330: 10,29 = 32,1.
Da forholdet mellem spændingsværdierne er 32,1, skal drejningsforholdet også være i samme format.
Betydning, x: 3 = 32,1, hvor x = sekundære vendinger, 3 = primære vendinger.
Løsning af dette kan vi hurtigt få det sekundære antal drejninger
Derfor er sekundære vendinger = 96,3.
Figur 96.3 er antallet af sekundære drejninger, som vi har brug for til den foreslåede ferritinvertertransformator, som vi designer. Som nævnt tidligere, da fraktionerede ventiler er vanskelige at implementere praktisk, afrunder vi den til 96 omdrejninger.
Dette afslutter vores beregninger, og jeg håber, at alle læsere her skal have indset, hvordan man simpelthen beregner en ferrittransformator til et specifikt SMPS-inverter kredsløb.
Beregning af hjælpevikling

En ekstravikling er en supplerende vikling, som en bruger kan kræve for en vis ekstern implementering.
Lad os sige, sammen med 330 V ved sekundær, har du brug for en anden vikling for at få 33 V til en LED-lampe. Vi beregner først sekundær: hjælpestøtte drejningsforhold i forhold til den sekundære vikling 310 V nominel værdi. Formlen er:
NTIL= Vsek/ (Vtil+ Vd)
NTIL= sekundær: hjælpeforhold, Vsek= Sekundær reguleret ensrettet spænding, Vtil= hjælpespænding, Vd= Diode fremad faldværdi for ensretterdioden. Da vi har brug for en højhastighedsdiode her, bruger vi en schottky-ensretter med en Vd= 0,5V
At løse det giver os:
NTIL= 310 / (33 + 0,5) = 9,25, lad os afrunde det til 9.
Lad os nu udlede antallet af drejninger, der kræves til hjælpeviklingen, vi får dette ved at anvende formlen:
Ntil= Nsek/ NTIL
Hvor Ntil= hjælpedrejninger, Nsek= sekundære drejninger, NTIL= hjælpeforhold.
Fra vores tidligere resultater har vi Nsek= 96, og NTIL= 9, der erstatter disse i ovenstående formel får vi:
Ntil= 96/9 = 10,66, afrunding giver os 11 drejninger. Så for at få 33 V skal vi bruge 11 omdrejninger på den sekundære side.
Så på denne måde kan du dimensionere en hjælpevikling efter din egen præference.
Afslutter
I dette indlæg lærte vi, hvordan man beregner og designer ferritkerne-baserede invertertransformatorer ved hjælp af følgende trin:
- Beregn primære sving
- Beregn sekundære sving
- Bestem og bekræft B maks
- Bestem den maksimale sekundære spænding til PWM-feedbackkontrol
- Find primært sekundært svingforhold
- Beregn sekundært antal omdrejninger
- Beregn hjælpevindinger
Ved hjælp af de ovennævnte formler og beregninger kan en interesseret bruger nemt designe en tilpasset ferritkernebaseret inverter til SMPS-applikation.
For spørgsmål og tvivl er du velkommen til at bruge kommentarfeltet nedenfor, jeg vil prøve at løse det tidligst
Forrige: Typer af Arduino-brædder med specifikationer Næste: Digital-til-analog (DAC), Analog-til-digital (ADC) -omformere forklaret