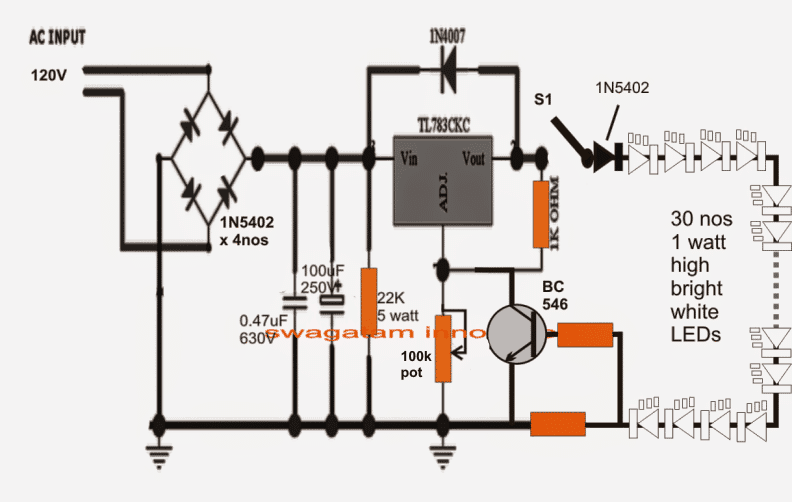
Darlington transistorberegninger

Darlington transistor er en velkendt og populær forbindelse ved hjælp af et par bipolar transistor junction transistor (BJT), designet til at fungere som en samlet 'fantastisk' transistor. Følgende diagram viser detaljerne i forbindelsen.

Definition

En Darlington-transistor kan defineres som en forbindelse mellem to BJT'er, der giver dem mulighed for at danne en enkelt sammensat BJT, der erhverver en betydelig mængde strømforstærkning, som typisk kan ligge ud over tusind.

Den største fordel ved denne konfiguration er, at den sammensatte transistor opfører sig som en enkelt enhed, der har en forbedret nuværende gevinst svarende til produktet af den aktuelle gevinst for hver transistor.

Hvis Darlington-forbindelsen består af to individuelle BJT'er med nuværende gevinster β₁og β_toden samlede strømforøgelse kan beregnes ved hjælp af formlen:

b_D= β₁b_to-------- (12.7)

Når matchede transistorer anvendes i en Darlington-forbindelse, således at β₁= β_to= β, den ovenstående formel for den aktuelle forstærkning bliver forenklet som:

b_D= β^to-------- (12.8)

Pakket Darlington Transistor

På grund af sin enorme popularitet er Darlington-transistorer også fremstillet og tilgængelige færdigt fremstillet i en enkelt pakke, der har to BJT'er internt forbundet som en enhed.

Den følgende tabel giver databladet for et eksempel på Darlington-par i en enkelt pakke.

Den angivne aktuelle gevinst er nettovinsten fra de to BJT'er. Enheden leveres med 3 standardterminaler eksternt, nemlig base, emitter, kollektor.

Denne form for pakkede Darlington-transistorer har eksterne funktioner, der ligner en normal transistor, men har meget høj og forbedret strømforøgelsesoutput sammenlignet med de normale single-transistorer.

Sådan DC Bias en Darlington Transistor Circuit

Den følgende figur viser et fælles Darlington-kredsløb ved hjælp af transistorer med en meget høj strømforstærkning β_D.

Her kan basisstrømmen beregnes ved hjælp af formlen:

jeg_B= V_DC- V_VÆRE/ R_B+ β_DR_ER-------------- (12.9)

Selv om dette kan ligne ligning, som normalt anvendes til enhver almindelig BJT , værdien β_Di ovenstående ligning vil være væsentligt højere, og V_VÆREvil være forholdsvis større. Dette er også bevist i eksemplet på datablad præsenteret i foregående afsnit.

Derfor kan emitterstrømmen beregnes som:

jeg_ER= (β_D+ 1) I_B≈ β_Djeg_B-------------- (12.10)

DC spænding vil være:

V_ER= Jeg_ERR_ER-------------- (12.11)

V_B= V_ER+ V_VÆRE-------------- (12.12)

Løst eksempel 1

Ud fra dataene i den følgende figur beregner du forspændingsstrømme og spændinger i Darlington-kredsløbet.

Opløsning : Ved anvendelse af ligning 12.9 bestemmes basisstrømmen som:

jeg_B= 18 V - 1,6 V / 3,3 MΩ + 8000 (390Ω) ≈ 2,56 μA

Ved anvendelse af ligning 12.10 kan emitterstrømmen evalueres som:

jeg_ER≈ 8000 (2,56 μA) ≈ 20,28 mA ≈ I_C

Emitter DC spænding kan beregnes ved hjælp af ligning 12.11 som:

V_ER= 20,48 mA (390Ω) ≈ 8 V,

Endelig kan kollektorspænding vurderes ved at anvende ækv. 12.12 som angivet nedenfor:

V_B= 8 V + 1,6 V = 9,6 V

I dette eksempel vil forsyningsspændingen ved opsamleren af ​​Darlington være:
V_C= 18 V.

AC-ækvivalent Darlington Circuit

I nedenstående figur kan vi se a BJT emitter-tilhænger kredsløb tilsluttet i Darlington-tilstand. Parterminalens basisterminal er forbundet til et vekselstrømsindgangssignal gennem kondensator C1.

Udgangssignalet, der opnås gennem kondensatoren C2, er forbundet med enhedens emitterterminal.

Simuleringsresultatet af ovenstående konfiguration er vist i den følgende figur. Her kan Darlington-transistoren ses erstattet med et vekselstrømsækvivalent kredsløb med en indgangsmodstand r _jeg og en udgangskilde for strøm repræsenteret som b _D jeg _b

AC-indgangsimpedansen kan beregnes som forklaret nedenfor:

AC basestrøm, der passerer igennem r _jeg er:

jeg_b= V_jeg- V_eller/ r_jeg---------- (12,13)

Siden
V_eller= (Jeg_b+ β_Djeg_b) R_ER---------- (12.14)

Hvis vi anvender ligning 12.13 i ligning. 12.14 får vi:

jeg_br_jeg= V_jeg- V_eller= V_jeg- Jeg_b(1 + β_D) R_ER

Løsning af ovenstående for V _jeg:

V_jeg= Jeg_b[r_jeg+ (1 + β_D) R_ER]

V_jeg/ Jeg_b= r_jeg+ β_DR_ER

Nu, når man undersøger transistorbasen, kan dens AC-indgangsimpedans evalueres som:

MED_jeg= R_B॥ r_jeg+ β_DR_ER---------- (12.15)

Løst eksempel 2

Lad os nu løse et praktisk eksempel på ovenstående AC-ækvivalent emitterfollower-design:

Bestem indgangsimpedansen til kredsløbet, givet r _jeg = 5 kΩ

Ved anvendelse af ligning 12.15 løser vi ligningen som angivet nedenfor:

MED_jeg= 3,3 MΩ॥ [5 kΩ + (8000) 390 Ω)] = 1,6 MΩ

Praktisk design

Her er et praktisk Darlington-design ved at forbinde en 2N3055 effekt transistor med et lille signal BC547 transistor.

Der bruges en 100K modstand på signalindgangssiden til at reducere strømmen til et par millamps.

Normalt med så lav strøm ved basen kan 2N3055 alene aldrig oplyse en høj strømbelastning såsom en 12V 2 amp pære. Dette skyldes, at den nuværende forstærkning på 2N3055 er meget lav for at behandle den lave basisstrøm til høj kollektorstrøm.

Men så snart en anden BJT, som er en BC547 her, er forbundet med 2N3055 i et Darlington-par, springer den samlede strømforøgelse op i en meget høj værdi og tillader lampen at lyse ved fuld lysstyrke.

Den gennemsnitlige strømforstærkning (hFE) på 2N3055 er omkring 40, mens den for BC547 er 400. Når de to kombineres som et Darlington-par, skyder gevinsten i det væsentlige op til 40 x 400 = 16000, er det ikke fantastisk. Det er den slags magt, vi er i stand til at få fra en Darlington-transistorkonfiguration, og en almindelig udseende transistor kunne omdannes til en meget klassificeret enhed bare med en simpel ændring.