Boolsk algebra-lommeregner er strømmen af matematik, der består af logiske udtryk og manipulering af logiske variabler. Det udfører logiske operationer som AND, NAND, OR, NOR, NOT & X-OR . Værdierne i den boolske algebra-lommeregner er angivet med logikken 0 & 1. Den boolske algebra-lommeregner bruger de grundlæggende love som identitetslov, kommutativ lov, distributionsret, associeret lov og afskedigelsesret. Hovedformålet med denne lov bruges til at udføre de logiske operationer som lighed, adskillelse, sammenhæng og implikation. De logiske operationer kan angives på forskellige måder, såsom: konjunktion (a ^ b) angives som a og b, disjunktion (a Vb) er angivet som a eller b, implikation (a b) angives som en antyder b & lighed (ab) er angivet som p x-nor q.

Boolsk algebra-lommeregner
Anvendelsen af boolsk algebra ligner en elektrisk omskiftertilstand, der enten kan være logiske værdier 0 og 1. Boolsk algebra-regnemaskine giver øjeblikkeligt resultatet i form af et matematisk udtryk ved at udføre operationerne som tilføjelse, multiplikation osv. Den boolske lommeregner er meget let og enkel at bruge. Boolean Algebra Calculator Block Diagram
Boolsk algebra lommeregner blokdiagram
Blokdiagrammet for boolsk algebra-regnemaskine indeholder forskellige blokke som Strømforsyning , tastatur, mikrocontroller og LED display .

Boolsk algebra lommeregner blokdiagram
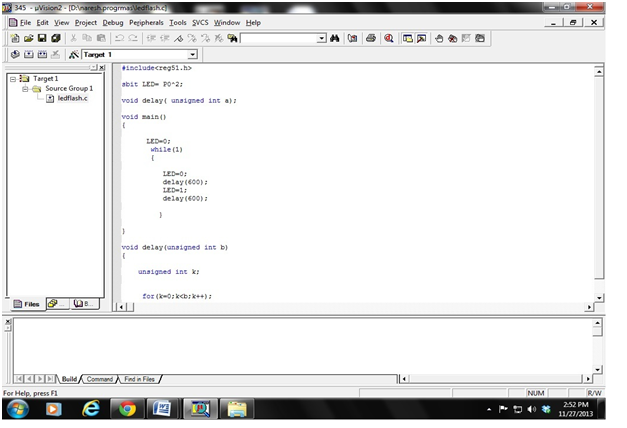
Strømforsyningen bruges til at give strømmen til uglekredsløbet, og den konverterer forskellige former for energier som solenergi, mekaniske og kemiske energier til elektrisk energi. Dette projekt bruger en 5V energi, og den gives til tastaturet, displayet og mikrocontrolleren. En mikrocontroller bruges til at læse dataene fra tastaturet og sender dataene til LCD-skærm . Mikrocontrolleren spiller en vigtig rolle i dette projekt, og det er programmeret af en Kile software .
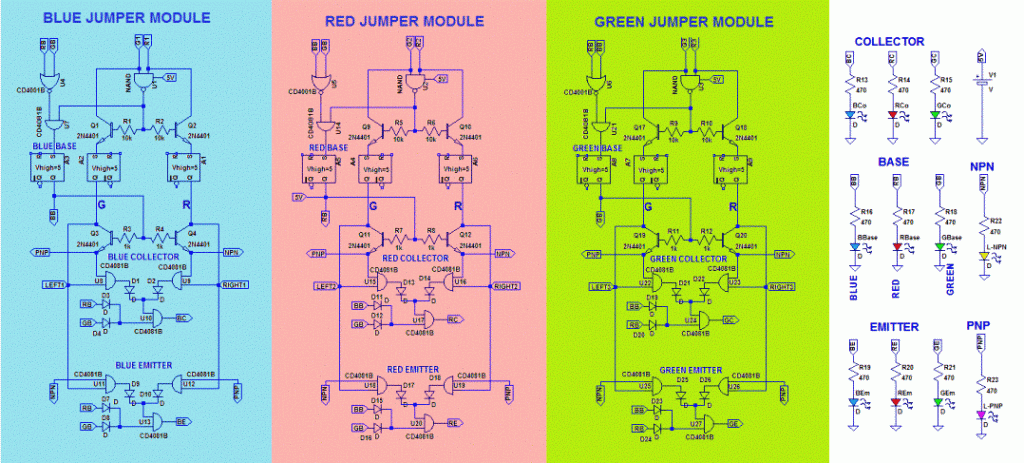
I dette projekt bruges en 3-bi-farvet LED-skærm til at vise udtrykkets glødende mønster. Disse Bi-farver betyder det normale og komplement af variabler som switches. Tastaturet i dette projekt bruges til at give min. Vilkår som i / p, dvs. hvert ciffer på tastaturet, der reagerer på hvert min.
Boolsk algebra lommeregner kredsløb
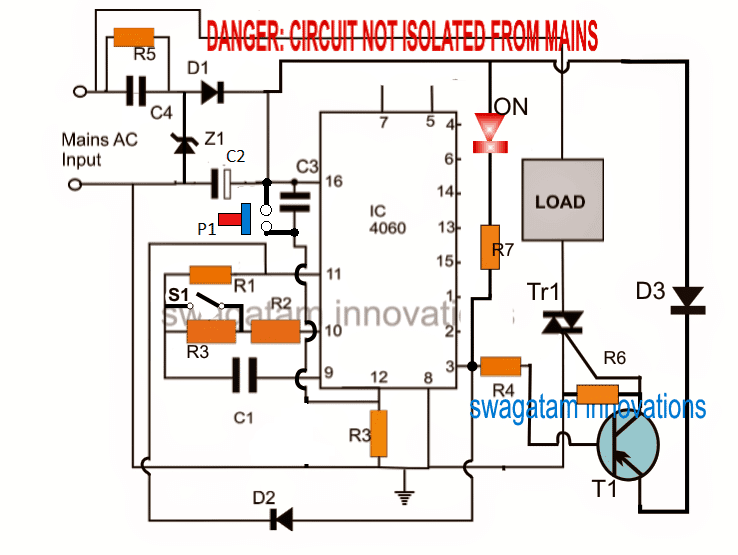
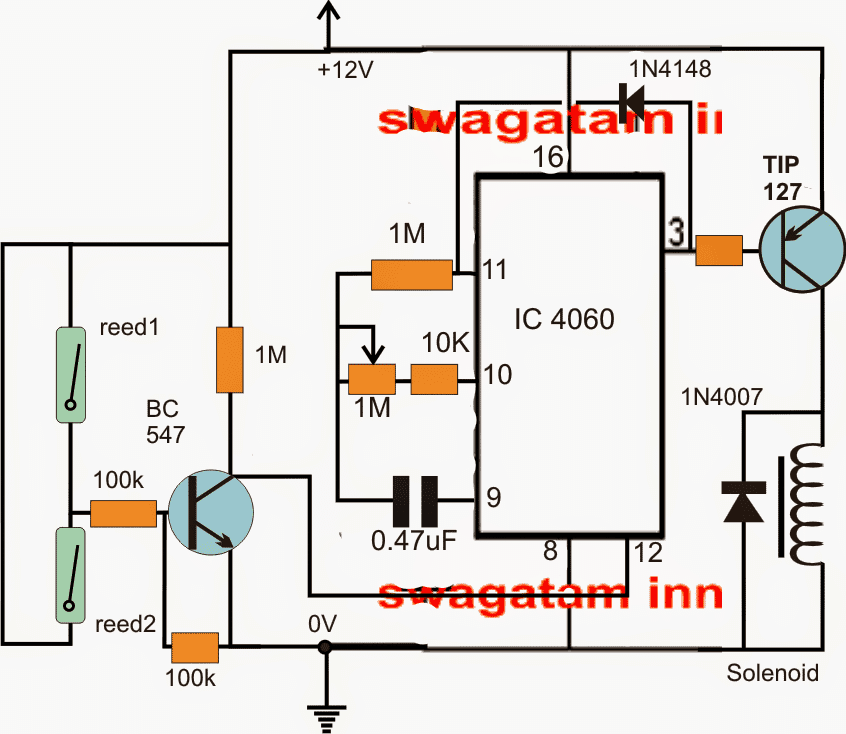
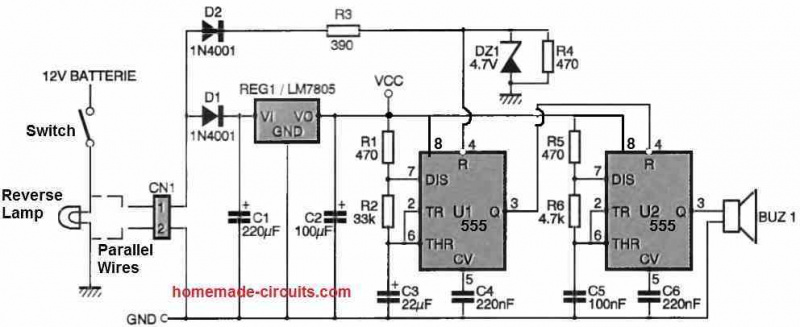
Følgende boolske algebra-lommeregner kredsløbsdiagram er billig, hurtig ydelse med lav effekt og pålidelig. Dette kredsløb er bygget med simpelt elektriske og elektroniske komponenter som er tilgængelige på markedet som modstande, tastatur, LCD-display og mikrokontroller som vist i det følgende kredsløb.

Boolsk algebra lommeregner kredsløb
Ovenstående kredsløb består af tre variable minimizer, der bruger 'Quine MC Cluskey-algoritmen' og finder min sum af produkter ved at udføre boolske funktioner. Denne lommeregner løser de boolske udtryk og logiske funktioner ved at bruge forskellige sætninger og love. Mikrocontrolleren, der bruges i dette projekt, spiller en vigtig rolle, der er kodet med et program og styrer de komponenter, der bruges i dette kredsløb.
Når strømforsyningen gives til kredsløbet, blinker LED'en. Den blinkende LED indikerer, at mikrokontrolleren er klar til at modtage i / ps fra tastaturet. Disse boolske udtryk gives i form af en sum af produkter (SOP).
Dette projekt bruger et tastatur, der består af 9 switche, hvor otte switche relateret til min termer, der udfører produktoperationen og den resterende switch bruges som den næste knap. Når udtrykket indtastes, slukkes LED'en, og baseret på algoritmen formindsker mikrokontrollen udtrykket på kort sigt. Derefter blinker i / p-LED'en, hvilket betyder, at udtrykket minimeres og vises på LED'en.
O / p vises som en min. Periode på én gang, og den anden min. Periode vises ved at trykke på den næste knap. Efter at have fået den sidste min. Periode, reduceres udtrykket, og i / p-LED'en slukkes, hvilket viser, at o / p bliver afsluttet. Derefter tænder LED automatisk for at indikere, at mikrokontrolleren er klar til at tage det videre s.
Forenkling af boolsk udtryk
Følgende udtryk er et eksempel på boolske udtryk ved hjælp af algebraiske teknikker.
Udtrykket er ~ (A * B) * (~ A + B) * (~ B + B) = ~ A
- ~ (A * B) * (~ A + B) * (~ B + B)
- Identitetsloven og komplementærloven er ~ (A * B) * (~ A + B).
- DeMorgan lov og (~ A ~ + B) * (~ A + B)
- Distributive Law er ~ A + ~ B * B
- ~ A er et kompliment eller en identitet.
Hvert eneste trin giver en ligningsform, og reglerne bruges til at løse ligningerne fra de tidligere ligninger. Generelt er der forskellige måder at nå resultatet på.
Boolske algebra love
Der er mange love at løse de boolske udtryk. De boolske algebra-sætninger er nemlig Idempotent Associative, Commutative, Distributive, Identity, Complement, Involution og DeMorgan's.
Idempotent lov
A * A = A
A + A = A
Associativ lov
(A * B) * C = A * (B * C)
(A + B) + C = A + (B * C)
Kommutativ lov
A * B = B * A
A + B = B + A.
Distributiv lov
A * (B + C) = A * B + A * C.
A + (B * C) = A + B * A + C.
Identitetslov
A * 0 = 0 A *! = A
A +! =! A + 0 = A.
Lov om komplimenter
A * ~ A = 0
A + ~ A =!
Involution Law
~ (~ A) = A
DeMorgan's lov
~ (A * B) = ~ A + ~ B
~ (A + B) = ~ A * ~ B
Hver lov i ovennævnte er beskrevet af to dele, og det er dualer af hinanden. Dualitetsprincippet er at udveksle + (OR) & * (AND) operationerne, 0 og 1 elementer i udtrykket.
For bedre forståelse af Boolean Algebra Calculator Circuit-koncept forklarede vi her en boolsk algebra-forenkling. Eksemplet på forenkling af boolsk algebra forklares nedenfor.

Eksempel på forenkling af boolsk algebra
Ovenstående kredsløb er designet med to OR- og to NAND-porte, fra kredsløbet kan vi få ligningen som AB + BC (B + C), der er vist i ovenstående figur. Når identitetsreglen og faktoriseringsfinalen anvendes på ovenstående kredsløb, vil det forenklede udtryk komme i form af simpelt.
Således handler det hele om Boolsk algebra lommeregner kredsløb, boolsk algebra lommeregner blokdiagram, boolsk algebra lommeregner kredsløb diagram, forenkling af boolsk udtryk, boolsk algebra love og boolsk algebra forenkling eksempel. Vi mener, at du har fået en bedre forståelse af dette koncept. Desuden er du i tvivl om dette emne. Giv din feedback ved at kommentere i kommentarfeltet nedenfor. Her er et spørgsmål til dig, hvad er anvendelserne af boolsk algebra-lommeregner?